Jordan), o sistema linear:
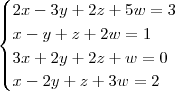
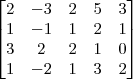
1º Passo
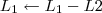
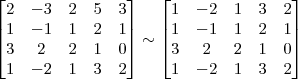
2º Passo
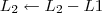
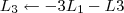
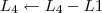
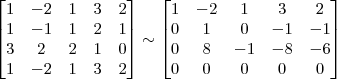
3º Passo
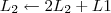
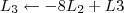
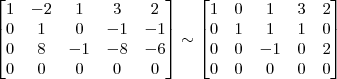
4º Passo

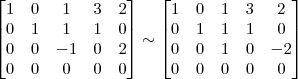
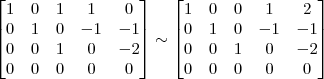
5º passo
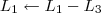
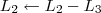
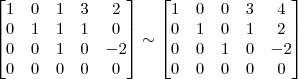
Consegui chegar até essa parte, alguém ajuda a concluir o exercício?

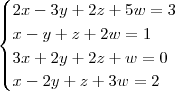
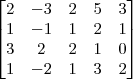
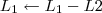
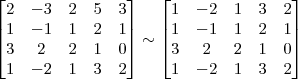
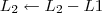
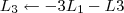
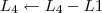
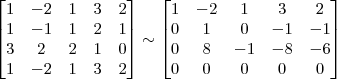
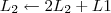
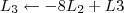
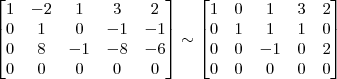

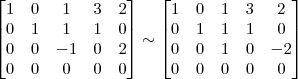
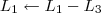
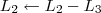
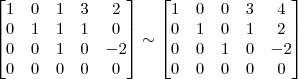

Claudin escreveu:2º Passo
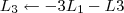 , entretanto você realizou a operação
, entretanto você realizou a operação 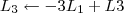 .
.Claudin escreveu:3º Passo
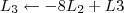
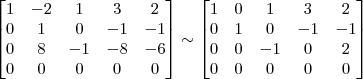


Claudin escreveu:Parece que fiz mais confusão ainda, se tiver como editar meu rascunho acima, deixando-o correto iria ajudar no entendimento, pois só fiz mais confusão com sua explicação.


Claudin escreveu:O que estou fazendo confusão seria porque você resolve buscando achar a matriz triangular superior no caso, já eu tento por outra forma, escalonando tudo, que é do jeito que meu professor pede na prova.


Claudin escreveu:Eu resolvo do mesmo modo expresso no vídeo, transformando a diagonal principal em 1.


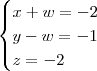


Claudin escreveu:O resultado que cheguei após a correção foi esse:
Caso continue errado, alguém ajude.
3º Passo)


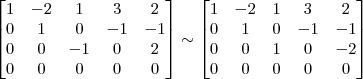
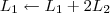
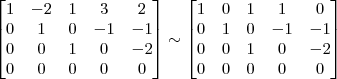
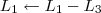
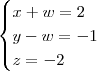


Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.