 por Rafael16 » Sáb Jul 14, 2012 21:44
por Rafael16 » Sáb Jul 14, 2012 21:44
Olá pessoal,
(F.M. ABC-SP) Em uma P.A., onde

e

, o primeiro termo é

e a razão é x, ache o valor de x
Resposta: 2
Fiz da seguinte forma, mas deu errado:
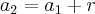
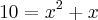

(I)
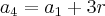
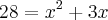
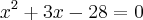
(II)
Joguei no sistema

(I)
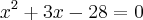
(II)
e achei

Gostaria de saber como errei.
Obrigado gente!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por DanielFerreira » Sáb Jul 14, 2012 22:00
por DanielFerreira » Sáb Jul 14, 2012 22:00
Rafael,
erroneamente, considerou

.
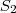
quer dizer: a soma dos dois primeiros termos.
Com isso,
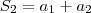

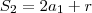
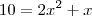
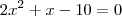
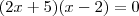
Analogamente,
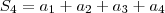
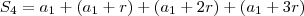
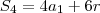
(...)
Deverá encontrar
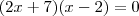
Note que a
(x - 2) = 0 é comum...
Espero ter ajudado!!
Comente qualquer dúvida.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Rafael16 » Sáb Jul 14, 2012 22:13
por Rafael16 » Sáb Jul 14, 2012 22:13
Hmmm, entendi, brigadão danjr5!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por DanielFerreira » Sáb Jul 14, 2012 22:19
por DanielFerreira » Sáb Jul 14, 2012 22:19
Não há de quê!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  , o primeiro termo é
, o primeiro termo é e a razão é x, ache o valor de x
e a razão é x, ache o valor de x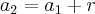
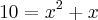
 (I)
(I)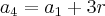
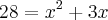
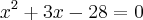 (II)
(II) (I)
(I)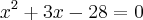 (II)
(II)

 e
e  , o primeiro termo é
, o primeiro termo é e a razão é x, ache o valor de x
e a razão é x, ache o valor de x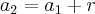
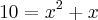
 (I)
(I)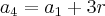
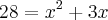
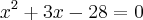 (II)
(II) (I)
(I)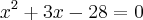 (II)
(II)

 .
.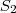 quer dizer: a soma dos dois primeiros termos.
quer dizer: a soma dos dois primeiros termos.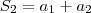

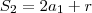
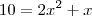
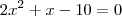
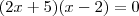
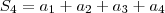
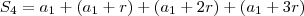
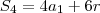
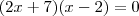





 , avisa que eu resolvo.
, avisa que eu resolvo.

