seja (a1, a2, ..., an) uma progressão geométrica com um número ímpar de termos e razão q>0. O produto de seus termos é igual a 2^25 e o termo do meio é 2^5. Se a soma dos (n-1) primeiros termos é igual a 2(1+q)(1+q^2), então :
a) a1 + q =16
b) a1 + q =12
c) a1 + q = 10
d) a1 + q + n = 20
e) a1 + q + n = 11


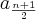 .
.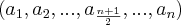 , (com razão q > 0.
, (com razão q > 0. ![{a}_{\frac{n+1}{2}} = \sqrt[]{{a}_{1}.{a}_{n}}\rightarrow{a}_{1}.{a}_{n} = \left({\frac{n+1}{2}} \right)^{2}\rightarrow{a}_{1}.{a}_{n} = \left({2}^{5} \right)^{2}\rightarrow{a}_{1}.{a}_{n} = {2}^{10} {a}_{\frac{n+1}{2}} = \sqrt[]{{a}_{1}.{a}_{n}}\rightarrow{a}_{1}.{a}_{n} = \left({\frac{n+1}{2}} \right)^{2}\rightarrow{a}_{1}.{a}_{n} = \left({2}^{5} \right)^{2}\rightarrow{a}_{1}.{a}_{n} = {2}^{10}](/latexrender/pictures/42a249fc87341f2b1483876f5cdc417e.png)
^{n}. P_n = \sqrt[]({{a}_{1}.{a}_{n}})^{n}.](/latexrender/pictures/9089f1edffbbc7dbbf385ef01a8f3008.png) .
. e
e 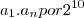 , vem:
, vem:^{n} P_n = \sqrt[]({{a}_{1}.{a}_{n}})^{n}](/latexrender/pictures/3cee16bf3fd36195f2480ce68ff01c57.png)
![\rightarrow{2}^{25} = \sqrt[]{({2}^{10})^{n}}\rightarrow{2}^{25} = \sqrt[]{({2}^{n})^{10}}\rightarrow{2}^{25} = {2}^{5n}\rightarrow 5n = 25\rightarrow n = 5 \rightarrow{2}^{25} = \sqrt[]{({2}^{10})^{n}}\rightarrow{2}^{25} = \sqrt[]{({2}^{n})^{10}}\rightarrow{2}^{25} = {2}^{5n}\rightarrow 5n = 25\rightarrow n = 5](/latexrender/pictures/47b155553c13709a733b7128e7bf23e1.png)
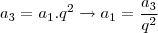
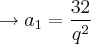
![{s}_{4} = \frac{{a}_{1\left({q}^{4}-1 \right)}}{\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left[\left({{q}^{2}} \right)^{2}-1 \right]}{{q}^{2}.\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left({q}^{2}-1 \right).\left({q}^{2}-1 \right)}{{q}^{2}.\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left({q}^{2}+1).\left(q+1 \right).\left(q-1 \right) \right)}{{q}^{2}.\left(q-1 \right)} {s}_{4} = \frac{{a}_{1\left({q}^{4}-1 \right)}}{\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left[\left({{q}^{2}} \right)^{2}-1 \right]}{{q}^{2}.\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left({q}^{2}-1 \right).\left({q}^{2}-1 \right)}{{q}^{2}.\left(q-1 \right)}\rightarrow{s}_{4} = \frac{32\left({q}^{2}+1).\left(q+1 \right).\left(q-1 \right) \right)}{{q}^{2}.\left(q-1 \right)}](/latexrender/pictures/618d67a08ac357403df758e435d7e13e.png)
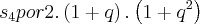 vem:
vem: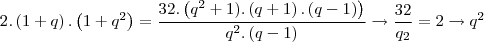 = 16 ? q = 4 ou q = -4 ( não convém, pois devemos ter q > 0 )
= 16 ? q = 4 ou q = -4 ( não convém, pois devemos ter q > 0 )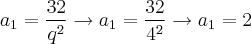

 .
.
 :
: