 por Cleyson007 » Sáb Set 26, 2009 19:23
por Cleyson007 » Sáb Set 26, 2009 19:23
Boa noite!
Estou encontrando dificuldade em resolver o exercício abaixo...
--> Numa reserva florestal foram computados 3.645 coelhos. Uma determinada
infecção alastra-se de modo que, ao final do primeiro dia, há cinco coelhos
infectados e, a cada cinco dias, o número total de coelhos infectados triplica.
a) Determine a quantidade de coelhos infectados ao final do 21° dia. R= 405
b) Calcule o número mínimo de dias necessário para que toda a população de
coelhos esteja infectada. R= 21
Alguém pode me ajudar?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Dom Set 27, 2009 18:02
por Molina » Dom Set 27, 2009 18:02
Olá Cleyson.
Pelo enunciado no primeiro dia há 5 coelhos infectados e a cada cinco diz multiplicamos este valor por 3, então:
a)
1° dia: 5
multiplicando por 3:6° dia: 15
multiplicando por 3:11° dia: 45
multiplicando por 3:16° dia: 135
multiplicando por 3:21° dia:
405Ou resolvendo por PG de razão 3:
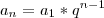
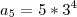

b) Resolvemos por PG também:
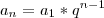
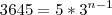

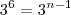

Note que 7 é o 7° dia da progressão (1, 6, 11, 16, ...)
Logo, o número mínimo de dias necessários para que todos os coelhos estejam infectados é
31 Confirma se não houve erro de digitação nesta b).

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Seg Set 28, 2009 18:34
por Cleyson007 » Seg Set 28, 2009 18:34
Boa tarde Molina!
Eu também estou achando estranho a resposta do gabarito..

(foi por esse motivo que resolvi postar a questão).
O gabarito deve estar errado
 Molina, obrigado pela ajuda!
Molina, obrigado pela ajuda!Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por shirata » Seg Out 05, 2009 12:18
por shirata » Seg Out 05, 2009 12:18
(ITA-SP) O valor de "n" que torna a sequencia (2 + 3n, - 5n, 1 - 4n) uma progressão aritmética pertence ao intervalo:
a) [-2, -1]
b) [-1, 0]
c) [0,1]
d) [1,2]
e) [2,3]
eu tentei fazendo
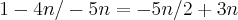
. Pois sendo uma PA a razão deverá ser igualpara a divisão entre o termo seguinte pelo anterior.
Aí cheguei na equação 37n2 + 5n -2 = 0, mas não consegui nenhum dos intervalos
-
shirata
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 05, 2009 11:25
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões
por Marcos Roberto » Sáb Out 15, 2011 21:57
- 0 Respostas
- 1502 Exibições
- Última mensagem por Marcos Roberto

Sáb Out 15, 2011 21:57
Progressões
-
- Progressões
por zenildo » Qui Out 10, 2013 22:54
- 1 Respostas
- 1971 Exibições
- Última mensagem por Cleyson007

Sex Out 11, 2013 15:27
Progressões
-
- Progressões
por verilane souza » Ter Set 30, 2014 16:32
- 1 Respostas
- 2111 Exibições
- Última mensagem por fff

Ter Set 30, 2014 18:22
Progressões
-
- progressões
por solon » Qui Jul 23, 2015 17:57
- 2 Respostas
- 4371 Exibições
- Última mensagem por solon

Sáb Ago 01, 2015 03:48
Progressões
-
- progressões
por solon » Ter Jul 21, 2015 01:56
- 2 Respostas
- 5178 Exibições
- Última mensagem por solon

Ter Jul 21, 2015 12:43
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



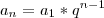
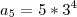

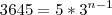

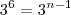



 (foi por esse motivo que resolvi postar a questão).
(foi por esse motivo que resolvi postar a questão).
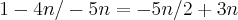 . Pois sendo uma PA a razão deverá ser igualpara a divisão entre o termo seguinte pelo anterior.
. Pois sendo uma PA a razão deverá ser igualpara a divisão entre o termo seguinte pelo anterior.

 , avisa que eu resolvo.
, avisa que eu resolvo.

