 por fabriel » Qua Out 31, 2012 11:32
por fabriel » Qua Out 31, 2012 11:32
E ai pessoal então: é dado essa questão:
"Determine três números de uma PG, conhecendo sua soma 19, e a soma de seus quadrados 133."
Sei que a soma dos termos de uma pg é dada:
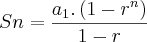
Então:
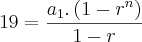
Posso deixar isso em função de (a1 e r)
Mas como será dos quadrados??
Obrigado!!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por fabriel » Qui Nov 01, 2012 01:34
por fabriel » Qui Nov 01, 2012 01:34
Obrigado. Agora vi a solução!!

PG:(4,6,9)
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas
 por Adriana Barbosa » Seg Jun 01, 2009 11:01
por Adriana Barbosa » Seg Jun 01, 2009 11:01
- 1 Respostas
- 1720 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 07:00
Funções
-
- duvidas e + duvidas
por sukita » Ter Out 05, 2010 22:22
- 1 Respostas
- 1671 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 22:31
Progressões
-
- Duvidas
 por Paulo A G » Qua Jan 26, 2011 14:45
por Paulo A G » Qua Jan 26, 2011 14:45
- 1 Respostas
- 3000 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:09
Pedidos de Materiais
-
- 2 dúvidas
por analuiza » Qui Fev 17, 2011 23:14
- 1 Respostas
- 2720 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:33
Trigonometria
-
- Dúvidas ....
por vanessa134 » Seg Out 17, 2011 01:06
- 0 Respostas
- 1511 Exibições
- Última mensagem por vanessa134

Seg Out 17, 2011 01:06
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
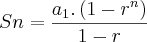
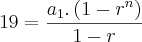

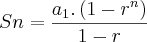
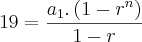

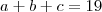
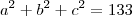
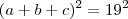
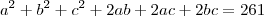
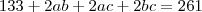
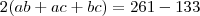









 , avisa que eu resolvo.
, avisa que eu resolvo.

