 por Colton » Dom Jul 25, 2010 17:39
por Colton » Dom Jul 25, 2010 17:39
+
+
"Quais as progressões aritméticas nas quais a soma de dois termos quaisquer faz parte da progressão?"
Se eu tomar dois termos quaisquer: [ap = a1+(p-1)*r] + [aq = a1+(q-1)*r] chego a ap+aq = 2a1+(p+q-1-1)*r mas aí eu "empaco"...a resposta do livro é a1 = k*r, k Inteiro, isto é o primeiro termo da progressão tem que ser múltiplo da razão o que é claro, pois aí qualquer termo será múltiplo de r, assim como a soma de quaisquer termos...só eu não vislumbro os passos de ap+aq = 2a1+(p+q-1-1)*r até a1 = k*r, k Inteiro.
Agradeço uma orientação.
Gratos
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
 por alexandre32100 » Qui Set 23, 2010 21:29
por alexandre32100 » Qui Set 23, 2010 21:29
Bom começo.
Vou usar este mesmo caminho.
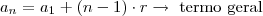
Dois termos aleatórios:
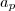
e
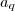
.

Compare a soma que você obteve com o termo geral.
Veja que na "fórumla" da soma de dois termos quaisquer temos
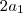
e na do termo geral, apenas
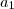
, assim,
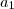
tem de ser divisível por

para que a soma dos dois seja um termo da PA, algo do tipo
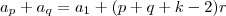
onde
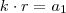
e é claro
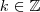
(usei

para ficar igual à solução do teu livro), afinal não existe o termo

numa progressão.
Não sei se consegui ser claro nessa explicação, mas é essa a ideia. Não creio que haja um forma
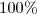
algébrica para isso.

-
alexandre32100
-
 por Colton » Sex Set 24, 2010 07:49
por Colton » Sex Set 24, 2010 07:49
+
+
Gratos, Alexandre.
Colton
+
+
-
Colton
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Jul 25, 2010 17:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


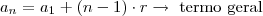
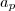 e
e 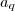 .
.
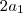 e na do termo geral, apenas
e na do termo geral, apenas 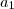 , assim,
, assim,  para que a soma dos dois seja um termo da PA, algo do tipo
para que a soma dos dois seja um termo da PA, algo do tipo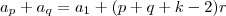 onde
onde 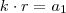 e é claro
e é claro 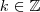 (usei
(usei  para ficar igual à solução do teu livro), afinal não existe o termo
para ficar igual à solução do teu livro), afinal não existe o termo  numa progressão.
numa progressão.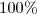 algébrica para isso.
algébrica para isso. 
