 por JKS » Qui Abr 11, 2013 01:54
por JKS » Qui Abr 11, 2013 01:54
preciso de ajuda,desde já agradeço!
Seja

um valor fixado no intervalo
![\left[0,\frac{\pi}{2} \right] \left[0,\frac{\pi}{2} \right]](/latexrender/pictures/1383a7ee0ed99beee339c92e7a5fae08.png)
. Sabe-se que a1=cotg

é o primeiro termo de uma PG infinita de razão q =
.A soma de todos os termos dessa progressão é :
gabarito : sec

.cossec

-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Qui Abr 11, 2013 13:27
por e8group » Qui Abr 11, 2013 13:27
A fórmula da Soma dos infinitos termos de uma progressão geométrica é :
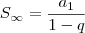
.
Caso tenha curiosidade de como chegar nesta fórmula ,veja :
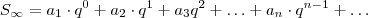
.
Ou ainda de forma compacta ,
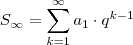
.
Agora note que
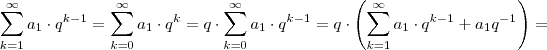

.
Daí ,somando-se
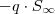
em ambos membros , temos
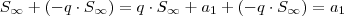
.
Como
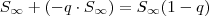
; desde que

,ou seja ,
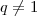
. Podemos ,multiplicar ambos membros por
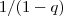
obtendo ,
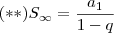
.
Aplicação para o exercício :
Condições para aplicarmos a fórmula
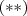
:
Como foi dado que
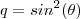
e
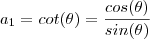
,temos então que
obrigatoriamente 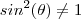
e

.
Assim ,

é um valor fixado no intervalo
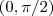
e não
![\left[0,\pi/2\right] \left[0,\pi/2\right]](/latexrender/pictures/4bb510c32589d41db3084fd07db1dcfd.png)
.Com estas condições podemos aplicar a fórmula
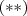
,segue
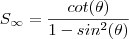
que devido a
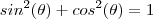
,
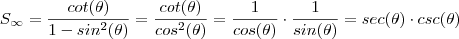
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma de uma PG infinita
por silvia fillet » Qua Fev 15, 2012 19:53
- 12 Respostas
- 9048 Exibições
- Última mensagem por Rosana Vieira

Qua Fev 22, 2012 17:44
Progressões
-
- [PG alternante e infinita]
por JKS » Qui Abr 11, 2013 01:24
- 3 Respostas
- 2447 Exibições
- Última mensagem por DanielFerreira

Sex Abr 26, 2013 21:30
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 2098 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:52
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 1889 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:49
Progressões
-
- Progressão geométrica (Soma da PG infinita)
por kellykcl » Qui Fev 27, 2014 23:20
- 2 Respostas
- 4064 Exibições
- Última mensagem por alexandre_de_melo

Sex Fev 28, 2014 17:07
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 um valor fixado no intervalo
um valor fixado no intervalo ![\left[0,\frac{\pi}{2} \right] \left[0,\frac{\pi}{2} \right]](/latexrender/pictures/1383a7ee0ed99beee339c92e7a5fae08.png) . Sabe-se que a1=cotg
. Sabe-se que a1=cotg  é o primeiro termo de uma PG infinita de razão q =
é o primeiro termo de uma PG infinita de razão q = 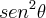 .A soma de todos os termos dessa progressão é :
.A soma de todos os termos dessa progressão é : .cossec
.cossec 

 um valor fixado no intervalo
um valor fixado no intervalo ![\left[0,\frac{\pi}{2} \right] \left[0,\frac{\pi}{2} \right]](/latexrender/pictures/1383a7ee0ed99beee339c92e7a5fae08.png) . Sabe-se que a1=cotg
. Sabe-se que a1=cotg  é o primeiro termo de uma PG infinita de razão q =
é o primeiro termo de uma PG infinita de razão q = 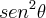 .A soma de todos os termos dessa progressão é :
.A soma de todos os termos dessa progressão é : .cossec
.cossec 

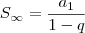 .
. 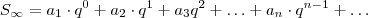 .
.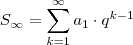 .
. 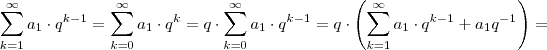
 .
. 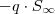 em ambos membros , temos
em ambos membros , temos 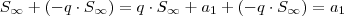 .
. 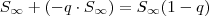 ; desde que
; desde que  ,ou seja ,
,ou seja , 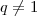 . Podemos ,multiplicar ambos membros por
. Podemos ,multiplicar ambos membros por 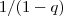 obtendo ,
obtendo , 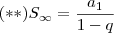 .
. 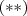 :
: 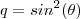 e
e 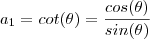 ,temos então que obrigatoriamente
,temos então que obrigatoriamente 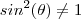 e
e  .
.  é um valor fixado no intervalo
é um valor fixado no intervalo 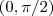 e não
e não ![\left[0,\pi/2\right] \left[0,\pi/2\right]](/latexrender/pictures/4bb510c32589d41db3084fd07db1dcfd.png) .Com estas condições podemos aplicar a fórmula
.Com estas condições podemos aplicar a fórmula 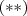 ,segue
,segue 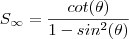 que devido a
que devido a 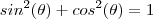 ,
, 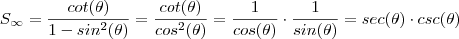 .
.
