 por joedsonazevedo » Sex Nov 09, 2012 11:49
por joedsonazevedo » Sex Nov 09, 2012 11:49
Olá, a questão que estou desenvolvendo é a seguinte...
Uma revendedora de automóveis observou que, em determinado ano, a venda de veículos automáticos aumentava, mensalmente, segundo uma progressão aritmética de razão 50. Considerando-se que, em junho, foram vendidas
320 unidades, pode se afirmar que o numero de veículos automáticos comercializados pela revendedora,
nesse ano, foi igual a
01) 690
02) 1380
03) 2070
04) 4140
05) 8280
Resolvi da seguinte forma:
(r= 50) (a6= 320) (a12 e a1= ?)
descobrindo a12 pela formula geral
--> an = a1 + (n+1)r
a6 = a12 +(6-12).50
320 = a12 - 300
a12= 620
descobrindo a1:
a6 = a1 + (6-1).50
320 = a1 + 250
a1 = 30
Utilizei a formula da Soma de termos para saber a soma
dos valores de carros vendidos nos 12 meses...
--> Sn = (a1+an).n => (30+620).12 => Sn = 3900
..............2.................2
porém não confere com o resultado do gabarito... que é 4140
gostaria de ajuda na interpretação da questão ou no próprio cálculo...
______________________________________________Muito Obrigado!
______________________________________________Joedson Azevedo
____________________________________________________________
-
joedsonazevedo
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qui Nov 08, 2012 14:23
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. em Informática
- Andamento: formado
 por young_jedi » Sex Nov 09, 2012 15:29
por young_jedi » Sex Nov 09, 2012 15:29
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6139 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4729 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5633 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4428 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8403 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



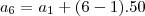
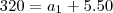
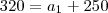


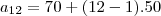

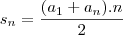
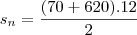
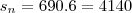

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.