resolví algumas questões,e outras nao deu,pq nao explicava bem na minha apostila!
se puder ajudar por favor,é urgente vo estudar mtooooo essas questoes...
lá vai...
1)um estacionamento cobra R$1,50 pela primeira hora.A partir da segunda,cujo valor é R$1,00 até a décima segunda,cujo valor é R$0,40,os preços caem em progressão aritmética.Se um automóvel ficar estacionado 5 horas nesse local,quanto gastará seu proprietário?
2)Uma progressão aritmetica de "n" termos tem razao igual a 3.se retirarmos os termos de ordem ímpar,os de ordem par formarão uma progressão aritmetica de razao igual a quanto?
3)Se os numeros 9,b e c são as medidas,em cm,dos lados de um triangulo retangulo e (9,b,c) formam, nesta ordem uma progressão aritmetica crescente,determine,em cm²,a medida da area do triangulo.
4)a soma dos 10 primeiros termos de uma progressão aritmetica é 185 e a soma dos 12 primeiros é 258.Determine o primeiro termo e a razão dessa progressao.
bjs=*
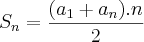
Abraços. 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)