por sonek182 » Qua Ago 19, 2009 17:51
Ola estou o dia todo tentando achar uma solução simples para essa função o que eu preciso e desenhar um grafico conforme a imagem em anexo, porem nao consigo localizar as cordenadas X e Y, atraves dos valores C e R e A
Estou tentando fazer por pitagoras se alguem tiver alguma solução melhor
O meu maior problema e que esse desenho e so uma parte do meu problema pois na verdade a figura completa vai ter 4 raios com caminhos tangentes ligando eles.
- Anexos
-
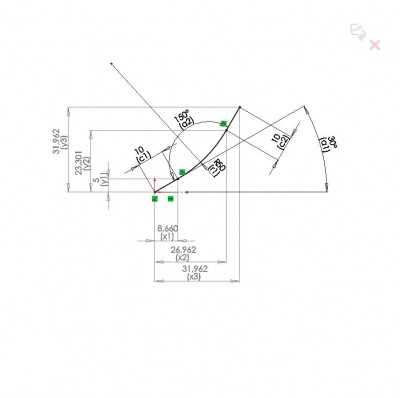
- Quebra cabeça
-
sonek182
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Qua Ago 19, 2009 16:41
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico mecanico
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Circulos Tangentes a Duas Retas
por nakagumahissao » Qua Abr 04, 2012 20:13
- 2 Respostas
- 3501 Exibições
- Última mensagem por nakagumahissao
Ter Mai 01, 2012 16:40
Sequências
-
- Retas tangentes ao gráfico
por Marcos_Mecatronica » Sáb Abr 27, 2013 19:58
- 1 Respostas
- 1873 Exibições
- Última mensagem por young_jedi
Dom Abr 28, 2013 12:16
Cálculo: Limites, Derivadas e Integrais
-
- [Geometria Plana] Circunferencia tangencida por duas retas
por stuartl » Dom Out 13, 2013 12:04
- 0 Respostas
- 1737 Exibições
- Última mensagem por stuartl
Dom Out 13, 2013 12:04
Geometria Plana
-
- retas tangentes
por kvothe » Sex Mai 06, 2011 17:48
- 1 Respostas
- 1845 Exibições
- Última mensagem por LuizAquino
Sex Mai 06, 2011 18:49
Cálculo: Limites, Derivadas e Integrais
-
- Retas tangentes à parabola
por Filipe Ricardo Rosa » Dom Jul 03, 2011 19:26
- 8 Respostas
- 9155 Exibições
- Última mensagem por LuizAquino
Qua Jul 06, 2011 10:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por
.
Temos que para
,
e para
,
.
Ache o valor de
e
, monte a função e substitua
por
.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!
ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
