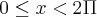 , a equação:
, a equação: 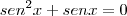 . Resposta: S={
. Resposta: S={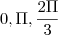 }
}Como tentei resolver:
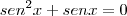
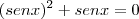

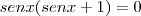
Raciocinio:
Uma multiplicação dando 0, então
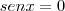 ou
ou  .*
.*O seno vale zero em 0º (0) e em 180º

OU o:

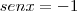
O seno de 270º
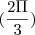 , vale -1
, vale -1O problema ocorre agora, como pensei em esse ou aquele vale zero *, não sei qual é o conjunto solução pois ambos podem zerar um dos termos.
Na verdade acho que o raciocinio (esse ou aquele vale zero) foi meio automatico e não sei pq estou fazendo ele, se houver outras formas de solucionar o problema, pode ser que clareie as minhas ideias.
Grato pela atenção,
Inté.


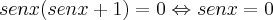 ou
ou 

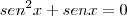 podemos passar o
podemos passar o 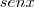 para o outro lado ficando:
para o outro lado ficando:
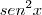 seja igual a
seja igual a 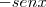 , no intervalo dado.
, no intervalo dado. , pelo menos para mim que pois sou bastante visual.
, pelo menos para mim que pois sou bastante visual. 