Então, eu tenho que resolver dois exercícios de trigonometria e não estou sabendo o que eu preciso fazer.
Eu NÃO QUERO SÓ COPIAR, eu realmente quero aprender, pois na prova vou precisar fazer, então eu gostaria que me explicassem os passos, nem precisa sei lá, resolver tudo, só queria saber o que eu preciso fazer.
Exercício 1: (U.F. Lavras - MG) O valor da expressão
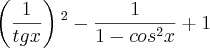 é de:
é de:a) sen²x
b) cos²x
c) 0
d) 1
e) 1/cos (x)
Exercício 2: (U.F. São Carlos-SP) O valor da expressão
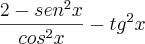 é:
é:a) -1
b) -2
c) 2
d) 1
e) 0


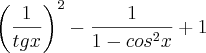 esse é o exercício.
esse é o exercício.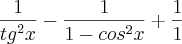
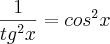
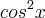 , alternativa b. Pelo menos eu tentei.
, alternativa b. Pelo menos eu tentei.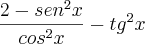
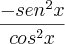 e coloquei o resultado como 1; 1 de novo, mas ok, KKKK, não achei saída. Como para mim, e acho que só para mim, a tg²x vale 1, ficou: 1 = - 1 que dá 2, então alternativa c.
e coloquei o resultado como 1; 1 de novo, mas ok, KKKK, não achei saída. Como para mim, e acho que só para mim, a tg²x vale 1, ficou: 1 = - 1 que dá 2, então alternativa c.

 .
.



