 por Cleyson007 » Seg Mar 29, 2010 13:07
por Cleyson007 » Seg Mar 29, 2010 13:07
Bom dia!
Se
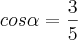
e
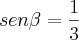
, com

pertencente ao terceiro quadrante e

pertencente ao segundo quadrante, calcular:
a)
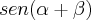
b)
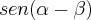
Calculei os valores de
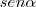
e
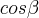
:

![cos\beta=\frac{2\sqrt[]{2}}{3} cos\beta=\frac{2\sqrt[]{2}}{3}](/latexrender/pictures/d5d37ba5e53c05499b1abde966870a13.png)
Resolvendo, encontrei:
![sen(\alpha+\beta)=\frac{8\sqrt[]{2}+3}{15} sen(\alpha+\beta)=\frac{8\sqrt[]{2}+3}{15}](/latexrender/pictures/d21ed5575c5e7a34b1c2d40b7adf29cb.png)
![sen(\alpha-\beta)=\frac{8\sqrt[]{2}+3}{15} sen(\alpha-\beta)=\frac{8\sqrt[]{2}+3}{15}](/latexrender/pictures/56b3393ddb8f22524e4853a82335909c.png)
Estou com dúvida na resposta devido falar que

pertencente ao terceiro quadrante e

pertencente ao segundo quadrante

Minha resolução está correta?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Elcioschin » Seg Mar 29, 2010 16:24
por Elcioschin » Seg Mar 29, 2010 16:24
Sua solução está ERRADA
Quando vc calculou sena deve ter chegado na seguinte equação ----> sen²a = 16/5 ---> sena = 4/5
Só que vc se esqueceu que, ao extrair a raiz quadrada vc deeria obter DUAS soluções ---> sena = + 4/5 ou sena = - 4/5
O sinal depende do quadrante !!!!
O mesmo vale para cálculo do senb
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Cleyson007 » Ter Mar 30, 2010 11:43
por Cleyson007 » Ter Mar 30, 2010 11:43
Bom dia prezado Elcio!
Realmente.. cometi esse erro!
Seria assim?
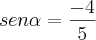
, observando a função seno:

No terceiro quadrante, o seno recebe valor negativo.
Quanto ao
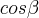
, observando a função cosseno:
Devido

pertencer ao segundo quadrante, deverá ser negativo:

Caro Elcio, o valor de
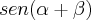
, será:
![\frac{8.\sqrt[]{2}+3}{15} \frac{8.\sqrt[]{2}+3}{15}](/latexrender/pictures/efd0965f0d35fca08c71f6cf98c477b6.png)
?
Antecipo agradecimentos.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Adição e Subtração de Arcos.
por DPeres » Sáb Mai 05, 2012 02:13
- 3 Respostas
- 2910 Exibições
- Última mensagem por LuizAquino

Dom Mai 06, 2012 09:05
Trigonometria
-
- Adição e Subtração de Arcos.
por DPeres » Sáb Mai 05, 2012 02:18
- 1 Respostas
- 1776 Exibições
- Última mensagem por LuizAquino

Sáb Mai 05, 2012 10:44
Trigonometria
-
- Adição e Subtração de Arcos.
 por DPeres » Sáb Mai 05, 2012 02:23
por DPeres » Sáb Mai 05, 2012 02:23
- 1 Respostas
- 1830 Exibições
- Última mensagem por LuizAquino

Sáb Mai 05, 2012 11:01
Trigonometria
-
- Adição e Subtração de Arcos.
por DPeres » Sáb Mai 05, 2012 02:38
- 1 Respostas
- 2167 Exibições
- Última mensagem por LuizAquino

Sáb Mai 05, 2012 11:20
Trigonometria
-
- Adiçao de Raizes
por vanessitah » Sáb Mar 05, 2011 18:38
- 8 Respostas
- 3715 Exibições
- Última mensagem por vanessitah

Dom Mar 06, 2011 00:58
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
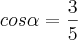 e
e 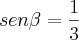 , com
, com  pertencente ao terceiro quadrante e
pertencente ao terceiro quadrante e  pertencente ao segundo quadrante, calcular:
pertencente ao segundo quadrante, calcular: 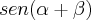
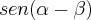
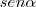 e
e 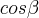 :
:
![cos\beta=\frac{2\sqrt[]{2}}{3} cos\beta=\frac{2\sqrt[]{2}}{3}](/latexrender/pictures/d5d37ba5e53c05499b1abde966870a13.png)
![sen(\alpha+\beta)=\frac{8\sqrt[]{2}+3}{15} sen(\alpha+\beta)=\frac{8\sqrt[]{2}+3}{15}](/latexrender/pictures/d21ed5575c5e7a34b1c2d40b7adf29cb.png)
![sen(\alpha-\beta)=\frac{8\sqrt[]{2}+3}{15} sen(\alpha-\beta)=\frac{8\sqrt[]{2}+3}{15}](/latexrender/pictures/56b3393ddb8f22524e4853a82335909c.png)
 pertencente ao terceiro quadrante e
pertencente ao terceiro quadrante e  pertencente ao segundo quadrante
pertencente ao segundo quadrante 



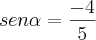 , observando a função seno:
, observando a função seno:

![\frac{8.\sqrt[]{2}+3}{15} \frac{8.\sqrt[]{2}+3}{15}](/latexrender/pictures/efd0965f0d35fca08c71f6cf98c477b6.png) ?
?