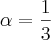 , então o valor de sen(25
, então o valor de sen(25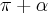 )-sen(88
)-sen(88 ):
):fiz a equivalência de sen 30°=1/2, mas não cheguei a lugar algum.

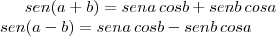
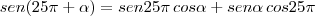
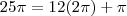 , ou seja, são 12 voltas completas mais "meia volta"
, ou seja, são 12 voltas completas mais "meia volta"  ; logo
; logo 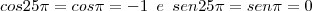
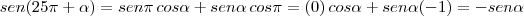
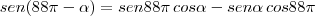
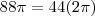 , que são 44 voltas completas, logo,
, que são 44 voltas completas, logo,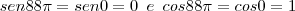
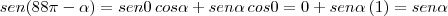
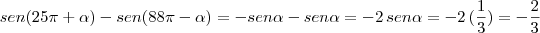

thadeu escreveu:Primeiro, utilize as propriedades:
Lembra do exercício passado??? No ciclo trigonométrico, ou seja, são 12 voltas completas mais "meia volta"
; logo
Substituindo na 1ª parte da expressão:
Na 2ª parte da expressão temos, que são 44 voltas completas, logo,
Substituindo na 2ª parte da expressão:
O resultado de expressão completa é:

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

