 por hbrunialti » Dom Mai 12, 2013 20:39
por hbrunialti » Dom Mai 12, 2013 20:39
Boa noite!
Estou resolvendo alguns exercicios de matemática das provas antigas da Fuvest e me deparei com uma situação que não sei mais que caminho seguir.
A questão é a 28 da fuvest 2013, e tem o seguinte enunciado:
---
Sejam

e

numeros reais com
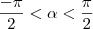
e
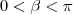
.
Se o sistema de equações, dado em notação matricial,
![\begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix} \begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix}](/latexrender/pictures/6a3c2a6c55cc22b760f01bd3b1c15914.png)
for satisfeito, então

é igual a:
---
A resposta correta é: -
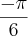
Na minha resolução, eu consegui resolver o sistema tudo certo e cheguei nas seguintes respostas:
tg

=
![- \sqrt[]{3} - \sqrt[]{3}](/latexrender/pictures/5146764d594e41cc1e0df3c201b01a02.png)
e cos

=
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
A partir daqui eu empaquei na resolução, olhando alguns sites que tem os exercicios resolvidos eles chegam a conclusão que
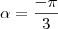
e
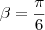
somente sabendo que um é tangente e outro é coseno e dai fazem a soma.
O que eu gostaria de entender é como eles conseguem descobrir os valores de

, e o que eu preciso estudar para ter conhecimento sobre esse assunto. Ja que eu não tenho nem certeza absoluta que isso é um problema para trigonometria.
Muito Obrigado!
-
hbrunialti
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 12, 2013 20:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por hbrunialti » Seg Mai 13, 2013 17:23
por hbrunialti » Seg Mai 13, 2013 17:23
Pessoal, consegui achar a resposta depois de penar muito, e vou responder aqui pra quem tiver a mesma duvida:
O cosseno de Beta consegue-se identificar pelo ciclo trigonometrico, sabendo que coseno de raiz de 3 sobre 2 é 30º o seu equivalente em radianos é pi sobre 6.
A tangente de menos raiz de 3 é 120 graus, que é oposto da tangente conhecida de raiz de 3 Por isso não estava conseguindo identificar. O segredo é você partir do 0º no sentido contrario tendo -60º logo menos pi sobre 3.
Dai é só fazer a soma.
-
hbrunialti
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 12, 2013 20:10
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- UCB 2013
 por Phaniemor » Qua Mai 01, 2013 11:36
por Phaniemor » Qua Mai 01, 2013 11:36
- 0 Respostas
- 922 Exibições
- Última mensagem por Phaniemor

Qua Mai 01, 2013 11:36
Geometria Plana
-
- QUESTÃO UCB 2013
por Phaniemor » Qua Mai 01, 2013 11:00
- 0 Respostas
- 1294 Exibições
- Última mensagem por Phaniemor

Qua Mai 01, 2013 11:00
Funções
-
- UCB 2013 questão 19
por Phaniemor » Qua Mai 01, 2013 11:07
- 0 Respostas
- 1483 Exibições
- Última mensagem por Phaniemor

Qua Mai 01, 2013 11:07
Funções
-
- probabilidade - UCB 2013
por Phaniemor » Qua Mai 01, 2013 11:11
- 0 Respostas
- 833 Exibições
- Última mensagem por Phaniemor

Qua Mai 01, 2013 11:11
Probabilidade
-
- ufpr 2013
por Maria Livia » Dom Out 13, 2013 11:40
- 0 Respostas
- 724 Exibições
- Última mensagem por Maria Livia

Dom Out 13, 2013 11:40
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  numeros reais com
numeros reais com 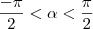 e
e 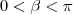 .
.![\begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix} \begin{pmatrix}
3 & 6 \\
6 & 8
\end{pmatrix} . \begin{pmatrix}
tg \alpha \\
cos \beta
\end{pmatrix} =
\begin{pmatrix}
0 \\
-2.\sqrt[]{3}
\end{pmatrix}](/latexrender/pictures/6a3c2a6c55cc22b760f01bd3b1c15914.png)
 é igual a:
é igual a: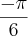
 =
= ![- \sqrt[]{3} - \sqrt[]{3}](/latexrender/pictures/5146764d594e41cc1e0df3c201b01a02.png)
 =
= ![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
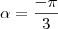 e
e 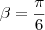 somente sabendo que um é tangente e outro é coseno e dai fazem a soma.
somente sabendo que um é tangente e outro é coseno e dai fazem a soma. , e o que eu preciso estudar para ter conhecimento sobre esse assunto. Ja que eu não tenho nem certeza absoluta que isso é um problema para trigonometria.
, e o que eu preciso estudar para ter conhecimento sobre esse assunto. Ja que eu não tenho nem certeza absoluta que isso é um problema para trigonometria.






