 por andersontricordiano » Seg Ago 08, 2011 18:45
por andersontricordiano » Seg Ago 08, 2011 18:45
Sabendo que
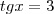
,
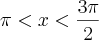
, calcule

Resposta:
![-\frac{\sqrt[]{10}}{5} -\frac{\sqrt[]{10}}{5}](/latexrender/pictures/39dfae2454f6667bb054114f6458959d.png)
-
andersontricordiano
- Colaborador Voluntário

-
- Mensagens: 192
- Registrado em: Sex Mar 04, 2011 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Abr 01, 2012 16:14
por DanielFerreira » Dom Abr 01, 2012 16:14
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Calculo de trigonometria) Calcule o valor da expressão
por andersontricordiano » Seg Dez 05, 2011 21:59
- 1 Respostas
- 2744 Exibições
- Última mensagem por nakagumahissao

Seg Abr 30, 2012 00:43
Trigonometria
-
- (Calculo de trigonometria) Calcule o valor de 4cosx/2senx
por andersontricordiano » Seg Ago 08, 2011 16:21
- 1 Respostas
- 1124 Exibições
- Última mensagem por MarceloFantini

Seg Ago 08, 2011 21:50
Trigonometria
-
- Calculo de trigonometria
 por andersontricordiano » Seg Jun 06, 2011 17:13
por andersontricordiano » Seg Jun 06, 2011 17:13
- 1 Respostas
- 5626 Exibições
- Última mensagem por claudinho

Sáb Jun 11, 2011 05:27
Geometria
-
- Calculo de trigonometria
por andersontricordiano » Qua Jun 29, 2011 19:37
- 1 Respostas
- 1259 Exibições
- Última mensagem por Molina

Qua Jun 29, 2011 20:30
Trigonometria
-
- Calculo de trigonometria
por andersontricordiano » Dom Jul 24, 2011 17:05
- 1 Respostas
- 1543 Exibições
- Última mensagem por FilipeCaceres

Dom Jul 24, 2011 18:01
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
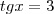 ,
,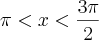 , calcule
, calcule 
![-\frac{\sqrt[]{10}}{5} -\frac{\sqrt[]{10}}{5}](/latexrender/pictures/39dfae2454f6667bb054114f6458959d.png)

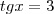 ,
,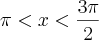 , calcule
, calcule 
![-\frac{\sqrt[]{10}}{5} -\frac{\sqrt[]{10}}{5}](/latexrender/pictures/39dfae2454f6667bb054114f6458959d.png)

,
, calcule
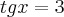
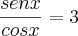
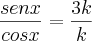
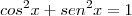
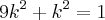
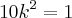
![k = \frac{1}{\sqrt[]{10}} k = \frac{1}{\sqrt[]{10}}](/latexrender/pictures/6a172e8d75df8871af02e4adf9e5288d.png) ou
ou ![k = - \frac{1}{\sqrt[]{10}} k = - \frac{1}{\sqrt[]{10}}](/latexrender/pictures/d5661c20805568091c84809d1051c5e9.png)
![sen x = \frac{3}{\sqrt[]{10}} sen x = \frac{3}{\sqrt[]{10}}](/latexrender/pictures/d0ff2fe2c2db7941a531ce0bde79a978.png) ou
ou ![sen x = - \frac{3}{\sqrt[]{10}} sen x = - \frac{3}{\sqrt[]{10}}](/latexrender/pictures/a6012942f5ddd56779b1cebc1bac8f07.png)
![cos x = \frac{1}{\sqrt[]{10}} cos x = \frac{1}{\sqrt[]{10}}](/latexrender/pictures/500dbb8923d7f7963db95b43eb984eaf.png) ou
ou ![cos x = - \frac{1}{\sqrt[]{10}} cos x = - \frac{1}{\sqrt[]{10}}](/latexrender/pictures/00074249fde51c19c79a35b995a1e97d.png)
![sen x = - \frac{3}{\sqrt[]{10}} sen x = - \frac{3}{\sqrt[]{10}}](/latexrender/pictures/a6012942f5ddd56779b1cebc1bac8f07.png)
![cos x = - \frac{1}{\sqrt[]{10}} cos x = - \frac{1}{\sqrt[]{10}}](/latexrender/pictures/00074249fde51c19c79a35b995a1e97d.png)
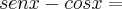
![- \frac{3}{\sqrt[]{10}} + \frac{1}{\sqrt[]{10}} = - \frac{3}{\sqrt[]{10}} + \frac{1}{\sqrt[]{10}} =](/latexrender/pictures/4874e2649447834e7f4f7f2ee66699fd.png)
![- \frac{2}{\sqrt[]{10}} = - \frac{2}{\sqrt[]{10}} =](/latexrender/pictures/cc8ed3a0bcbf753a296787351b079344.png)
![- \frac{2}{\sqrt[]{10}} . \frac{\sqrt[]{10}}{\sqrt[]{10}}= - \frac{2}{\sqrt[]{10}} . \frac{\sqrt[]{10}}{\sqrt[]{10}}=](/latexrender/pictures/ede6e6487e3c90de9be0da796b0eca12.png)
![- \frac{2\sqrt[]{10}}{10} = - \frac{2\sqrt[]{10}}{10} =](/latexrender/pictures/0189688491a5833a98e3bb1f24b23055.png)
![- \frac{\sqrt[]{10}}{5} = - \frac{\sqrt[]{10}}{5} =](/latexrender/pictures/8fc852d3d065eb9f5c99c090383eeb1a.png)

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.