 por Faria » Ter Ago 09, 2011 23:36
por Faria » Ter Ago 09, 2011 23:36
Boa noite pessoal, não estou conseguindo resolver esses dois exercícios.
Agradeço atenção.
Abç,
Faria.
1º Se
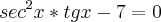
e 0 < x <
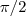
, então o valor de sec x será?
2º O dobro do seno de um ângulo x, 0 < x <
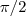
, é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno será?
-
Faria
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Mai 21, 2011 16:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em processamento de dados
- Andamento: formado
 por MarceloFantini » Sex Set 23, 2011 18:55
por MarceloFantini » Sex Set 23, 2011 18:55
Bom, não sei se é para deixar em função das outras funções trigonométricas, mas no primeiro exercício podemos fazer:
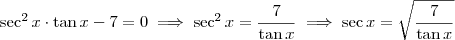
No segundo, equacionando temos que:

Tente fazer lembrando que

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 3158 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 4156 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 3436 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
-
- Equações
por Neperiano » Qua Fev 11, 2009 12:33
- 6 Respostas
- 6502 Exibições
- Última mensagem por marcio silva

Sex Mar 20, 2009 20:15
Sistemas de Equações
-
- Equações
por Luna » Qui Set 10, 2009 19:30
- 2 Respostas
- 2274 Exibições
- Última mensagem por Luna

Sex Set 11, 2009 19:54
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
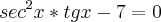 e 0 < x <
e 0 < x < 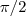 , então o valor de sec x será?
, então o valor de sec x será?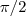 , é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno será?
, é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno será?
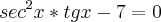 e 0 < x <
e 0 < x < 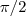 , então o valor de sec x será?
, então o valor de sec x será?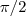 , é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno será?
, é igual ao triplo do quadrado de sua tangente. Logo, o valor de seu cosseno será?
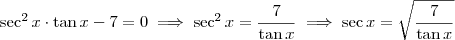

 .
.


 .
.
 :
: