Isto vai parecer estranho.
No desenvolvimento de um logaritmo Tenho:
, (eu sei que 
) então eu passei o expoente 2 do x para trás do log e penso que ficaria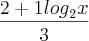 
, que por sua vez tem que ficar 
(este é o resultado final que tem de dar).O que eu quero saber é se a passagem do expoente para antes do log está correcta. Se o 2 passa a somar e não a multiplicar.
Esta dúvida surge por causa da propriedade que indiquei, em que o expoente passa a multiplicar pelo log e não a somar, como eu fiz.
E depois não percebo, no resultado final, porque o 3 fica a somar pelo log e não a multiplicar!
Obrigada
. Por favor, poste a questão completa e os passos que você deu até agora.
![{log}_{2}(2\sqrt[3]{x}](/latexrender/pictures/9127eb52a3f40170417c0e2412035170.png "{log}_{2}(2\sqrt[3]{x}")
)
=
=
=
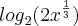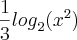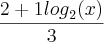que vai dar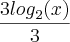 
![g(x)={log}_{2}(2\sqrt[3]{x})](/latexrender/pictures/310b09a4d9500b672b72811bfd7d56f7.png "g(x)={log}_{2}(2\sqrt[3]{x})")
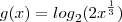
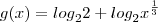
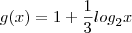
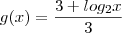
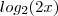, veja: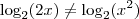
![\log_{2} (2 \sqrt[3]{x} ) \Rightarrow \, \log_{2}2 + log_{2} (\sqrt[3]{x}) \Rightarrow \, 1 + \frac{\log_{2}x}{3} \Rightarrow \, \frac{3 + \log_{2}x}{3}](/latexrender/pictures/1602b9f4f3c4b6006db386a7de88952a.png "\log_{2} (2 \sqrt[3]{x} ) \Rightarrow \, \log_{2}2 + log_{2} (\sqrt[3]{x}) \Rightarrow \, 1 + \frac{\log_{2}x}{3} \Rightarrow \, \frac{3 + \log_{2}x}{3}")
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.