 por Kirie » Seg Out 04, 2010 22:27
por Kirie » Seg Out 04, 2010 22:27
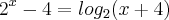
Mesmo após substituiçãode dos termos por ``Y`` não consigo isolar ``X``. Quem puder, agradeço desde já.
-
Kirie
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 04, 2010 22:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheiro
- Andamento: formado
 por MarceloFantini » Seg Out 04, 2010 23:01
por MarceloFantini » Seg Out 04, 2010 23:01
Essa é a equação original? Se possível, por favor poste o enunciado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Kirie » Ter Out 05, 2010 23:08
por Kirie » Ter Out 05, 2010 23:08
Fantini, essa equação é original, foi retirada do Livro do Cursinho Objetivo,Vestibular MACKENZIE não relacionando o ano, segue o Enunciado:
(MACK) As soluções reais da Equação (............) estão nos intervalos:
a){-4,-3} e {1,2}
b){-3,-2} e {2,3}
c){-4,-3} e {3,4}
d){-4,-3} e {2,3}
e){-2,-1} e {1,2}
Também não encontrei um método para resolução, exceto o gráfico. Se encontrar por favor me avise ! um abraço e agradeço pela atenção !
-
Kirie
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Out 04, 2010 22:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheiro
- Andamento: formado
 por MarceloFantini » Ter Out 05, 2010 23:34
por MarceloFantini » Ter Out 05, 2010 23:34
É como eu disse no outro post: o método realmente é o gráfico. Veja que ele não pede as raízes exatas, apenas uma idéia de onde elas se encontram.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UF-PA)Encontre a solução real da equação logaritmica
por andersontricordiano » Qua Set 28, 2011 11:23
- 1 Respostas
- 1492 Exibições
- Última mensagem por andersontricordiano

Sex Set 30, 2011 18:30
Logaritmos
-
- Solução da inequação logarítmica
 por Marcela123 » Sáb Set 12, 2009 02:29
por Marcela123 » Sáb Set 12, 2009 02:29
- 1 Respostas
- 2591 Exibições
- Última mensagem por Lucio Carvalho

Sáb Set 12, 2009 08:25
Logaritmos
-
- Encontrar Solução Geral de um Sis. Linear
por Jhonata » Qui Mai 02, 2013 16:09
- 3 Respostas
- 1949 Exibições
- Última mensagem por e8group

Qui Mai 02, 2013 18:01
Álgebra Linear
-
- Inequação - encontrar conjunto solução
 por rafaleans » Sex Mar 14, 2014 09:45
por rafaleans » Sex Mar 14, 2014 09:45
- 1 Respostas
- 1620 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 19, 2014 22:56
Inequações
-
- Qual é o conjunto solução da inequação logarítmica
por andersontricordiano » Sex Dez 02, 2011 14:53
- 1 Respostas
- 1868 Exibições
- Última mensagem por TheoFerraz

Sex Dez 02, 2011 15:22
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
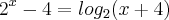

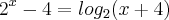






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.