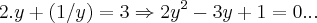por adauto martins » Sex Out 18, 2019 23:26
por adauto martins » Sex Out 18, 2019 23:26
(UFRRJ-universidade federal rural do rj-exame vestibular 1961)
resolva a equaçao
![2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})} 2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}](/latexrender/pictures/7db52e8bc30ba3d6d0eb7008413fd34d.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Out 19, 2019 00:48
por adauto martins » Sáb Out 19, 2019 00:48
soluçao:
![2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}=3.\sqrt[2n]{(1-x).(1+x)} 2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}=3.\sqrt[2n]{(1-x).(1+x)}](/latexrender/pictures/e2daf63b020c475f5b15f5f72add6f09.png)
![(2.\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)}=3
(2.\sqrt[n]{(1-x)})/(\sqrt[2n]{(1-x).(1+x)})+(\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)})=3 (2.\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)}=3
(2.\sqrt[n]{(1-x)})/(\sqrt[2n]{(1-x).(1+x)})+(\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)})=3](/latexrender/pictures/77ed2318e404966d66b903f71b8a5811.png)
sabendo que:
![\sqrt[n]{(1-x)}/\sqrt[2n]{(1-x)(1+x)}=(1-x)^{((1/n))}/((1-x)^{(1/2n)}.(1+x)^{(1/2n)})=(1-x)^{((1/n)-(1/2n))}/(1+x)^{(1/2n)}=(1-x)^{(1/2n)}/(1+x)^{(1/2n)}
=\sqrt[2n]{(1-x)/(1+x)} \sqrt[n]{(1-x)}/\sqrt[2n]{(1-x)(1+x)}=(1-x)^{((1/n))}/((1-x)^{(1/2n)}.(1+x)^{(1/2n)})=(1-x)^{((1/n)-(1/2n))}/(1+x)^{(1/2n)}=(1-x)^{(1/2n)}/(1+x)^{(1/2n)}
=\sqrt[2n]{(1-x)/(1+x)}](/latexrender/pictures/1f035d1d38e1b6d5c31d5560034c9790.png)
fazendo
![y=\sqrt[2n]{(1-x)/(1+x)} y=\sqrt[2n]{(1-x)/(1+x)}](/latexrender/pictures/1779efbeec5e4260fc719f00f7ba287f.png)
teremos:
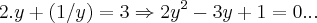
achar os valores de y,e consequentemente os valores de x...termine-o
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})} 2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}](/latexrender/pictures/7db52e8bc30ba3d6d0eb7008413fd34d.png)

![2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})} 2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}](/latexrender/pictures/7db52e8bc30ba3d6d0eb7008413fd34d.png)

![2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}=3.\sqrt[2n]{(1-x).(1+x)} 2\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)}=3\sqrt[2n]{(1-{x}^{2})}=3.\sqrt[2n]{(1-x).(1+x)}](/latexrender/pictures/e2daf63b020c475f5b15f5f72add6f09.png)
![(2.\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)}=3
(2.\sqrt[n]{(1-x)})/(\sqrt[2n]{(1-x).(1+x)})+(\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)})=3 (2.\sqrt[n]{(1-x)}+\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)}=3
(2.\sqrt[n]{(1-x)})/(\sqrt[2n]{(1-x).(1+x)})+(\sqrt[n]{(1+x)})/(\sqrt[2n]{(1-x).(1+x)})=3](/latexrender/pictures/77ed2318e404966d66b903f71b8a5811.png)
![\sqrt[n]{(1-x)}/\sqrt[2n]{(1-x)(1+x)}=(1-x)^{((1/n))}/((1-x)^{(1/2n)}.(1+x)^{(1/2n)})=(1-x)^{((1/n)-(1/2n))}/(1+x)^{(1/2n)}=(1-x)^{(1/2n)}/(1+x)^{(1/2n)}
=\sqrt[2n]{(1-x)/(1+x)} \sqrt[n]{(1-x)}/\sqrt[2n]{(1-x)(1+x)}=(1-x)^{((1/n))}/((1-x)^{(1/2n)}.(1+x)^{(1/2n)})=(1-x)^{((1/n)-(1/2n))}/(1+x)^{(1/2n)}=(1-x)^{(1/2n)}/(1+x)^{(1/2n)}
=\sqrt[2n]{(1-x)/(1+x)}](/latexrender/pictures/1f035d1d38e1b6d5c31d5560034c9790.png)
![y=\sqrt[2n]{(1-x)/(1+x)} y=\sqrt[2n]{(1-x)/(1+x)}](/latexrender/pictures/1779efbeec5e4260fc719f00f7ba287f.png)