Boa Noite.
Comecei a resolver esse exercício e cheguei num sistema, ficou muito grande. Desisti porque achei que fiz errado. Podem me ajudar, por favor? Obrigada pela ajuda!!
Se x e y são números naturais satisfazendo log(8) x + log(4)y² = 6 e log(4)x² + log(8)y = 10, qual o valor de ?xy? (os números entre parêntesis são as bases).


 então
então 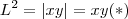 .Aplicamos o logaritmo (de base 8) em ambos os membros teremos
.Aplicamos o logaritmo (de base 8) em ambos os membros teremos 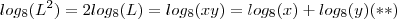 .
. 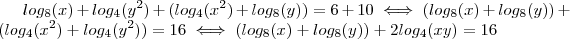 .
.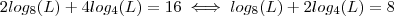 .
. 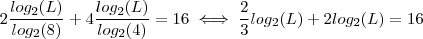 .
. 

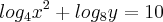
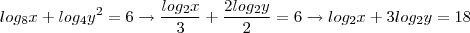
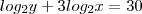
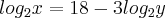
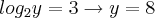
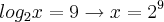
![\sqrt[]{8.{2}^{9}} = \sqrt[]{{2}^{12}} = \sqrt[]{2.2.2.2.2.2.2.2.2.2.2.2} = {2}^{6} = 64 \sqrt[]{8.{2}^{9}} = \sqrt[]{{2}^{12}} = \sqrt[]{2.2.2.2.2.2.2.2.2.2.2.2} = {2}^{6} = 64](/latexrender/pictures/0047172265ca7629fc0c84ed04814e8f.png)

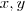 ...vejamos
...vejamos 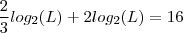 então
então ![log_2(L)[\frac{1}{3} + 1] =8 log_2(L)[\frac{1}{3} + 1] =8](/latexrender/pictures/befba3c0a81192a150c8f71a8491b0e7.png) então
então 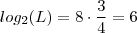 e assim
e assim 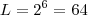 .
. 
 .
.
 :
: