-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480646 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542078 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 505798 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 734275 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2178365 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por matheus_frs1 » Seg Mai 12, 2014 21:43
por matheus_frs1 » Seg Mai 12, 2014 21:43
Não sei se é exatamente log que tem que usar, mas parti desse princípio...
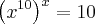
Tentei usar a propriedade de mudança de base e cheguei em
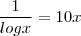
mas não consegui sair daqui. Alguém poderia me ajudar?
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Seg Mai 12, 2014 23:37
por Russman » Seg Mai 12, 2014 23:37
O seu princípio não está correto.
O certo é
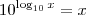
.
Note que as funções
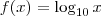
e
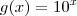
são uma a inversa da outra. Isto é,
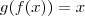
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Ter Mai 13, 2014 00:20
por matheus_frs1 » Ter Mai 13, 2014 00:20
Mas Russman, a propriedade do log não é assim:
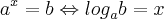
Então, eu fiz isso, veja:
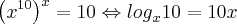
Depois usei a mudança de base para chegar em
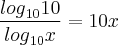
, e como log de 10 é 1 eu cheguei naquilo q te mandei.
Estou totalmente errado?
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Ter Mai 13, 2014 23:03
por Russman » Ter Mai 13, 2014 23:03
OK, sua definição de logaritmo está correta.
Agora, uma pergunta: A expressão
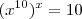
é uma equação? Isto é, você busca um valor

tal que
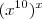
seja igual a

? Veja que esta expressão
não é uma identidade!!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Qua Mai 14, 2014 21:30
por matheus_frs1 » Qua Mai 14, 2014 21:30
Exatamente, Russman, é uma questão desafio para achar o valor de x. Só que a questão é muito esquisita, pq o mesmo x que está na base, tá lá no expoente. Joguei no Wolfram e ele me deu
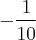
, mas não mostrou o processo de cálculo.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Qua Mai 14, 2014 23:55
por Russman » Qua Mai 14, 2014 23:55
Ah, sendo uma equação então faz sentido!
Você não é o 1° a buscar uma solução para este tipo de equação. A sua equação é resolvida através de uma função conhecida como Função W de Lambert. Assim como a velha e boa função logarítmica, esta função é uma função transcendental e os pontos de sua imagem são calculados por Séries de Taylor. Em outras palavras: a solução da sua equação não é algébrica e não basta conhecer as funções exponencial e logarítmica para resolvê-la.
matheus_frs1 escreveu:Depois usei a mudança de base para chegar em , e como log de 10 é 1 eu cheguei naquilo q te mandei.
Você pode chegar nesta expressão mais rapidamente! Aplique a função logaritmo
de base 10 (

)na equação. Assim, a expressão obtida é
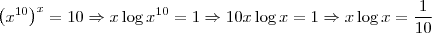
A expressão
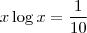
possui a solução exata dada por
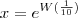
onde

é a tal Função W de Lambert e

é o Número de Euler.
Isto dá aproximadamente
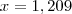
. De fato, calculando
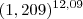
você obtém
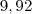
aproximadamente. Note que com 3 casas de precisão obtemos um erro +-0,07 no valor exato. Não é de todo mal.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Qui Mai 15, 2014 00:19
por matheus_frs1 » Qui Mai 15, 2014 00:19
Vish, não faço ideia do que seja isso, deve ser de matemática superior, né? Mesmo assim, vlw, Russman, vc é craque em matemática, hein?
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Qui Mai 15, 2014 23:38
por Russman » Qui Mai 15, 2014 23:38
É, matemática do ensino superior. Mas não se deixe impressionar, apenas apaixonar! hahah. Essa função W está no mesmo saco que as funções logarítmica, exponencial, seno e cosseno que, certamente,pela boa argumentação sobre o desenvolvimento das propriedades do logaritmo que me escreveu , você deve estar acostumado a manipular. Portanto, utilizá-la é também uma questão de tempo de costume. (:
Bons estudos!!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Dom Mai 18, 2014 15:29
por matheus_frs1 » Dom Mai 18, 2014 15:29
Russman, me conte mais sobre essa função W de Lambert...
Todo equação do tipo
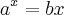
eu tenho que usar esse raciocínio?
Por exemplo,
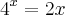
, tenho x no expoente do primeiro membro e x no segundo membro também. Se sim, gostaria de saber como devo proceder nesses tipos de exercícios, pq eu não entendi mto bem a resolução e também não encontrei vídeos a respeito.
Se não for muito incomodo, você pode me ensinar um "passo-a-passo"?
Obrigado.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Dom Mai 18, 2014 22:49
por Russman » Dom Mai 18, 2014 22:49
Uma equação do tipo
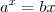
pode ser resolvida usando a Função W de Lambert.
Partamos da sua definição.
Se
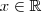
é tal que
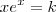
,
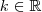
então
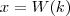
.
Ou seja,
se existir solução(ões) para a equação do tipo
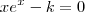
(1) então nossa esperança é que ao menos uma seja obtida pela função W de Lambert.
A sua equação pode ser escrita dessa forma fazendo uma
mudança de variável conveniente. Isto é, vamos mudar da variável

para uma outra

. Mas antes, caso você não o conheça, vamos falar de

.Este número

é o chamado Número de Euler. É um número irracional. É com ele que se define a
função exponencial 
. Note que podemos usar esta função para escrever qualquer outra função de potência em qualquer outra base. Da definição de função logarítmica podemos escrever que
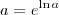
onde
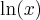
é a função logarítmica de base

.
Assim, podemos começar a transformar a sua equação da forma
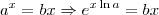
.
Você lembra que para quaisquer Reais
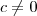
e

vale
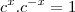
? Então, vamos multiplicar a expressão obtida em ambos membros por
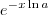
:
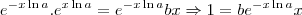
Estamos quase lá!! Para colocar, finalmente, a equação na forma desejada (1) basta agora multiplicá-la por
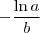
. Veja
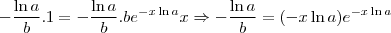
Pronto! Se você tomar
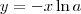
e
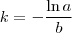
, então a equação acima se muda para
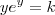
que é exatamente o tipo de equação resolvida pela Função W de Lambert.
Portanto, temos
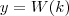
de onde, fazendo a substituição inversa
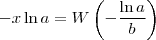
que calcula
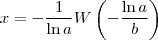
Se você deseja solucionar a equação
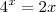
basta tomar,como eu imagino que você saiba,
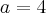
e

. Assim,
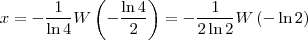
Esta
seria a solução. Entretanto, examinando melhor a equação
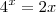
notamos que ela não possui solução Real. :(
É fácil de notar isto. Faça o gráfico de
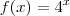
e sobreponha ao gráfico de
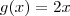
. Você verá que a função
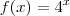
cresce muito rapidamente de modo que a função
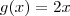
não a consegue alcançar em nenhum ponto

. Isto é, não existe
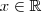
tal que

.
Um caso interessante é considerar a equação
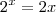
. Repetindo o processo de graficar as funções nota-se facilmente que esta equação tem duas soluções

e

. É fácil de verificar. De fato,
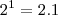
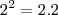
Aplicando a função W temos a solução
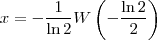
.
Agora, este número vale
 ou
ou 
ou nenhum destes( no caso de termos azar). Da própria definição de função não pode existir dois valores para um mesmo

. Então a função W fornece ao menos uma raiz(ou nenhuma) da equação, como eu citei antes.
Mais ou menos isso que você queria?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por sayurimatsuo » Seg Mai 19, 2014 11:20
por sayurimatsuo » Seg Mai 19, 2014 11:20
Pessoal, alguém conhece um site onde eu possa tirar dúvida sobre finanças?
Estou com complicação no meu fluxo de caixa, não consigo realizar as contas direito, e o sistema está desconfigurado.
Achei esta empresa, Cenize, alguém conhece?
http://cenize.com/jfinancas/controle-fi ... mpresarialObrigada!
-
sayurimatsuo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 21, 2014 15:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Finanças
- Andamento: formado
 por matheus_frs1 » Qui Mai 29, 2014 10:21
por matheus_frs1 » Qui Mai 29, 2014 10:21
Caramba, Russman... a primeira vista assim (pra quem nunca viu matemática a nível de ensino superior) parece um tanto complicadinho. Mas obrigado por me esclarecer, vou tentar aplicar em algum outro exercício. Se for uma receitinha de bolo, acho q dá pra resolver algumas questões seguindo esse seu processo. Obrigado, Russman.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6150 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 10876 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 14847 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 3985 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3024 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
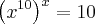
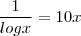 mas não consegui sair daqui. Alguém poderia me ajudar?
mas não consegui sair daqui. Alguém poderia me ajudar?
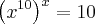
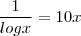 mas não consegui sair daqui. Alguém poderia me ajudar?
mas não consegui sair daqui. Alguém poderia me ajudar?
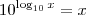 .
.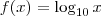 e
e 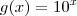 são uma a inversa da outra. Isto é,
são uma a inversa da outra. Isto é,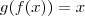

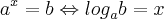
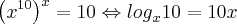
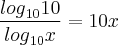 , e como log de 10 é 1 eu cheguei naquilo q te mandei.
, e como log de 10 é 1 eu cheguei naquilo q te mandei.
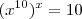 é uma equação? Isto é, você busca um valor
é uma equação? Isto é, você busca um valor  tal que
tal que 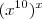 seja igual a
seja igual a  ? Veja que esta expressão não é uma identidade!!
? Veja que esta expressão não é uma identidade!!
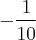 , mas não mostrou o processo de cálculo.
, mas não mostrou o processo de cálculo.
 )na equação. Assim, a expressão obtida é
)na equação. Assim, a expressão obtida é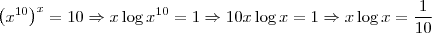
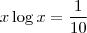 possui a solução exata dada por
possui a solução exata dada por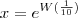
 é a tal Função W de Lambert e
é a tal Função W de Lambert e  é o Número de Euler.
é o Número de Euler.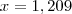 . De fato, calculando
. De fato, calculando 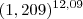 você obtém
você obtém 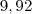 aproximadamente. Note que com 3 casas de precisão obtemos um erro +-0,07 no valor exato. Não é de todo mal.
aproximadamente. Note que com 3 casas de precisão obtemos um erro +-0,07 no valor exato. Não é de todo mal.


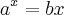 eu tenho que usar esse raciocínio?
eu tenho que usar esse raciocínio?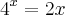 , tenho x no expoente do primeiro membro e x no segundo membro também. Se sim, gostaria de saber como devo proceder nesses tipos de exercícios, pq eu não entendi mto bem a resolução e também não encontrei vídeos a respeito.
, tenho x no expoente do primeiro membro e x no segundo membro também. Se sim, gostaria de saber como devo proceder nesses tipos de exercícios, pq eu não entendi mto bem a resolução e também não encontrei vídeos a respeito. 
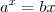 pode ser resolvida usando a Função W de Lambert.
pode ser resolvida usando a Função W de Lambert.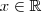 é tal que
é tal que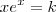 ,
, 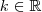
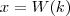 .
.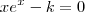 (1) então nossa esperança é que ao menos uma seja obtida pela função W de Lambert.
(1) então nossa esperança é que ao menos uma seja obtida pela função W de Lambert. para uma outra
para uma outra  . Mas antes, caso você não o conheça, vamos falar de
. Mas antes, caso você não o conheça, vamos falar de  .Este número
.Este número  é o chamado Número de Euler. É um número irracional. É com ele que se define a função exponencial
é o chamado Número de Euler. É um número irracional. É com ele que se define a função exponencial  . Note que podemos usar esta função para escrever qualquer outra função de potência em qualquer outra base. Da definição de função logarítmica podemos escrever que
. Note que podemos usar esta função para escrever qualquer outra função de potência em qualquer outra base. Da definição de função logarítmica podemos escrever que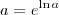
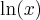 é a função logarítmica de base
é a função logarítmica de base  .
.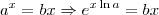 .
.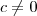 e
e  vale
vale 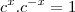 ? Então, vamos multiplicar a expressão obtida em ambos membros por
? Então, vamos multiplicar a expressão obtida em ambos membros por 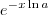 :
: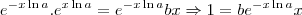
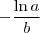 . Veja
. Veja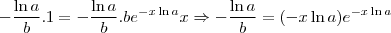
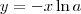 e
e 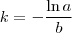 , então a equação acima se muda para
, então a equação acima se muda para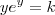
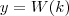
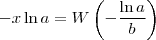
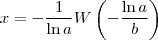
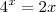 basta tomar,como eu imagino que você saiba,
basta tomar,como eu imagino que você saiba, 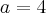 e
e  . Assim,
. Assim, 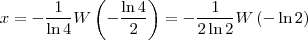
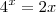 notamos que ela não possui solução Real. :(
notamos que ela não possui solução Real. :(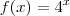 e sobreponha ao gráfico de
e sobreponha ao gráfico de 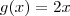 . Você verá que a função
. Você verá que a função 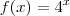 cresce muito rapidamente de modo que a função
cresce muito rapidamente de modo que a função 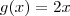 não a consegue alcançar em nenhum ponto
não a consegue alcançar em nenhum ponto  . Isto é, não existe
. Isto é, não existe 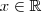 tal que
tal que  .
.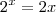 . Repetindo o processo de graficar as funções nota-se facilmente que esta equação tem duas soluções
. Repetindo o processo de graficar as funções nota-se facilmente que esta equação tem duas soluções e
e  . É fácil de verificar. De fato,
. É fácil de verificar. De fato,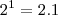
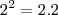
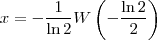 .
. ou
ou  ou nenhum destes( no caso de termos azar). Da própria definição de função não pode existir dois valores para um mesmo
ou nenhum destes( no caso de termos azar). Da própria definição de função não pode existir dois valores para um mesmo  . Então a função W fornece ao menos uma raiz(ou nenhuma) da equação, como eu citei antes.
. Então a função W fornece ao menos uma raiz(ou nenhuma) da equação, como eu citei antes.




 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
