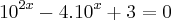 é:
é:A) 4
B) 1 + log3
C) log2 + log3
D) log5
E) log3
N?o consegui chegar no resultado, alguem pode me ajudar?

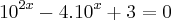 é:
é:
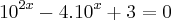
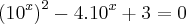
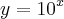
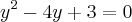
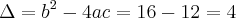
![y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2} y = \frac{-b \pm \sqrt[]{\Delta}}{2a} = \frac{4 \pm 2}{2}](/latexrender/pictures/0e20c2db16a4f409f0cf7302b992e0b0.png)


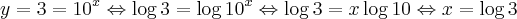
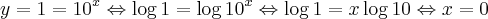

nakagumahissao escreveu:
Pelas propriedades da potenciação, podemos reescrever a equação acima da seguinte forma:
[1]
Agora, podemos fazer a seguinte substituição:
[2]
Substituindo [2] em [1], tem-se que:
e
Utilizando estes valores obtidos em [1] acima, tem-se que
a) Para y = 3:
e
b) Para y = 1:
PORTANTO, a soma das raízes da equação dada será: 1 + log(3), ou seja, a resposta é a letra (B)


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: