 por rhaytzmann » Ter Jun 03, 2014 17:18
por rhaytzmann » Ter Jun 03, 2014 17:18
Oi gente, preciso de ajuda nesse exercício:
"Se o logaritmo decimal de 7,5 é 0,875, o número de algarismos de
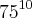
é:"
O gabarito é 19.
Eu desenvolvi o log de 75 e tal e achei 18,75, mas no gabarito ele fala que 18 é característica desse logaritmo e que, portanto
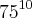
é 18+1 = 19.
Não entendi de onde saiu esse um e que característica é essa. Agradeço se puderem me ajudar porque só falta esse exercício pra eu terminar minha lista de log.
-
rhaytzmann
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Mai 29, 2014 18:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por blaze » Ter Jun 03, 2014 20:46
por blaze » Ter Jun 03, 2014 20:46
Partes da igualdade
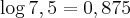
e fazes chegar até
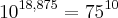
, que é o que aparece no enunciado. Ora,
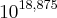
é um número com 18 casas decimais depois da vírgula, então os algarismos são esses tais 18 mais o que está à esquerda da vírgula, daí ser 18+1
-
blaze
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 07, 2014 17:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Mackenzie)
por my2009 » Sex Jan 28, 2011 21:28
- 1 Respostas
- 2693 Exibições
- Última mensagem por 0 kelvin

Sáb Jan 29, 2011 18:57
Logaritmos
-
- (Mackenzie) P.A. com P.G.
por Rafael16 » Sáb Ago 04, 2012 14:19
- 3 Respostas
- 10084 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:20
Progressões
-
- Mackenzie
por Maria Livia » Qua Fev 27, 2013 22:29
- 1 Respostas
- 33671 Exibições
- Última mensagem por Cleyson007

Qua Fev 27, 2013 22:41
Geometria Espacial
-
- (MACKENZIE-SP)
por Thiago 86 » Qua Mar 27, 2013 23:23
- 4 Respostas
- 3221 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 06, 2013 21:03
Inequações
-
- Questão (MACKENZIE)
por Carolziiinhaaah » Qua Jun 16, 2010 12:04
- 1 Respostas
- 3453 Exibições
- Última mensagem por Elcioschin

Qua Jun 16, 2010 13:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
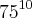 é:"
é:"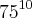 é 18+1 = 19.
é 18+1 = 19.

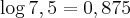 e fazes chegar até
e fazes chegar até 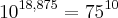 , que é o que aparece no enunciado. Ora,
, que é o que aparece no enunciado. Ora, 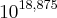 é um número com 18 casas decimais depois da vírgula, então os algarismos são esses tais 18 mais o que está à esquerda da vírgula, daí ser 18+1
é um número com 18 casas decimais depois da vírgula, então os algarismos são esses tais 18 mais o que está à esquerda da vírgula, daí ser 18+1 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
