Minha dúvida é no (-1), eu tenho q transformar em log? n sei oq fazer xP
se fosse sem o (-1) daria log(x³.2.y)
A resposta ta como log((x³.2.y)/b)
ps: todos os logs estão na base "b"
Me expliquem como chegar nisso plis..
Desde já agradeço


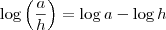 .
. , então
, então 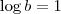 , certo? Assim,
, certo? Assim, 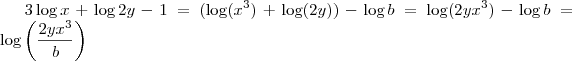 .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)