(mackenzie) se
 (2 na base x), então
(2 na base x), então  pertence ao intervalo:
pertence ao intervalo:
 (2 na base x), então
(2 na base x), então  pertence ao intervalo:
pertence ao intervalo:

 então
então  .
.  .
. 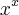 pertence ao intervalo ? " .
pertence ao intervalo ? " .  então
então 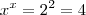 . logo qualquer intervalo contido em
. logo qualquer intervalo contido em  tais que o elemento
tais que o elemento  pertence a um destes estes intervalos satisfaz o enunciado . Como por exemplo
pertence a um destes estes intervalos satisfaz o enunciado . Como por exemplo ![[4,9) , [4,7] , [4,9) , [4,7] ,](/latexrender/pictures/7d81387f21b56fd09a660ec0c23c1b04.png) e assim por diante ;portanto cabe analisar cada alternativa se é que têm .
e assim por diante ;portanto cabe analisar cada alternativa se é que têm .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)