Olá, estou estudando matemática para obter um desempenho satisfatório no vestibular. Agradeço a ajuda.
Uma pessoa adquiriu uma calça jeans e observou que ela perde 2,5% de sua cor a cada lavagem, de tal modo que, após n lavagens, terá apenas 25% de sua cor original. Considerando, se necessário, log 5 = 0,698 e log 39 = 1,591, pode-se estimar que o valor aproximado de n é:
01) 10
02) 19
03) 28
04) 37
05) 46
Fazendo uma regra de três básica marquei 10 como sendo a resposta, mas o gabarito afirma que é 46.


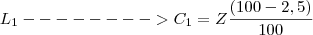
![L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2 L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2](/latexrender/pictures/533ddebba6ca81a6cf0a3a78821c2b93.png)
![L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n](/latexrender/pictures/7b0acc492195171677fa479eb7995e7a.png) ,como
,como 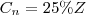 então ,
então ,![Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z](/latexrender/pictures/08cf233f5af9b01a52452f5a6e5f462e.png) . Aplicando Logaritmo de base 10 em ambos membros da equação temos :
. Aplicando Logaritmo de base 10 em ambos membros da equação temos :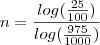 , ou seja
, ou seja 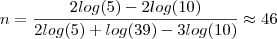



 .
.
 :
: