Pois estou tentando usar ln mas chega uma hora que eu travo, poderiam me ajudar?
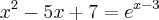

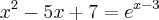




carvalhothg escreveu:Como resolver o exercício abaixo sem uso de computador, ou seja, como encontrar o valor de x na munheca?
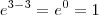 . Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que 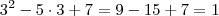 . Logo, x = 3 é uma solução dessa equação.
. Logo, x = 3 é uma solução dessa equação.
LuizAquino escreveu:carvalhothg escreveu:Como resolver o exercício abaixo sem uso de computador, ou seja, como encontrar o valor de x na munheca?
Essa é uma equação transcendental. Tipicamente, as equações transcendentais não possuem solução analítica. Isto é, usando a sua expressão: não dá para resolver "na munheca" essas equações. Portanto, é necessário aplicar métodos numéricos ou gráficos para resolvê-las. Entretanto, uma primeira estratégia é procurar por soluções triviais.
Note que o valor mais trivial que podemos pensar para o segundo membro da equação é quando x = 3, pois teremos. Precisamos agora verificar se para x = 3 o primeiro membro da equação também resulta em 1. De fato, temos que
. Logo, x = 3 é uma solução dessa equação.
Se houver outra solução, então ela não é mais trivial e algum método numérico ou gráfico deve ser aplicado. Por exemplo, aplicando o Método de Newton podemos encontrar que outra raiz dessa equação é aproximadamente x = 4,7933.
Aproveito ainda para lembrar que nos cursos de graduação da área de exatas há uma disciplina chamada Cálculo Numérico. Um dos objetivos dessa disciplina é exatamente aprender técnicas numéricas que permitem calcular a solução de equações como essa.



carvalhothg escreveu:Aquino,
primeiramente muito obrigado pela ajuda....sem quer abusar muito da sua boa vontade...você poderia ensinar a utilizar este método de newton?


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

