 por Aliocha Karamazov » Seg Abr 11, 2011 22:15
por Aliocha Karamazov » Seg Abr 11, 2011 22:15
Pessoal, não consigo encontrar uma solução para esse exercício:
Resolver a equação:
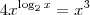
O problema é que eu não sei o que fazer com o 4, para deixar tudo na mesma base.
Agradeço a quem puder ajudar!
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por FilipeCaceres » Seg Abr 11, 2011 22:36
por FilipeCaceres » Seg Abr 11, 2011 22:36
Dica:
Faça,
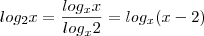
, não se esqueça de cuidar com as condições de existência.
E sabendo que,
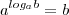
Agora tente desenvolver o resto.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 23:06
por Aliocha Karamazov » Seg Abr 11, 2011 23:06
Não entendi como você chegou a essa relação:
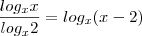
Eu conheço essa propriedade:
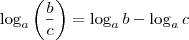
Não entendi bem o que você fez. Poderia explicar melhor? Obrigado.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por FilipeCaceres » Seg Abr 11, 2011 23:13
por FilipeCaceres » Seg Abr 11, 2011 23:13
Desculpaaaa,
Viajei loucamente, fiquei pensando agora da onde eu tirei isso, acho que deve ter bebido algo quando postei

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Aliocha Karamazov » Seg Abr 11, 2011 23:17
por Aliocha Karamazov » Seg Abr 11, 2011 23:17
Sem problemas. Você consegue outra forma de resolver esse exercício?
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por Fabricio dalla » Seg Abr 11, 2011 23:54
por Fabricio dalla » Seg Abr 11, 2011 23:54
engraçado pega aquele expoente em logaritimo e faz que log de base 2 logaritimando x=y tem se

ai substitui que cai numa equaçao exponencial ai vc acha y´=1 e y''=2 eu acho que o unico que convem e o 2 prq e o unico que atende a propriedade que felipe tinha falado de uma base com expoente logaritimo etc..
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Abr 12, 2011 00:35
por FilipeCaceres » Ter Abr 12, 2011 00:35
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por Aliocha Karamazov » Ter Abr 12, 2011 18:17
por Aliocha Karamazov » Ter Abr 12, 2011 18:17
Muito obrigado pela ajuda.
-
Aliocha Karamazov
- Usuário Parceiro

-
- Mensagens: 90
- Registrado em: Qua Mar 16, 2011 17:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2577 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- Exercício de logaritmo
por Aliocha Karamazov » Sáb Abr 09, 2011 01:24
- 2 Respostas
- 1364 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Abr 09, 2011 01:54
Logaritmos
-
- Exercicio de Logaritmo...
por torilleon » Qui Fev 16, 2012 18:47
- 1 Respostas
- 1174 Exibições
- Última mensagem por ant_dii

Qui Fev 16, 2012 18:51
Logaritmos
-
- [Aplicação de Logaritmo em Eq. Exponenciais] Exercício
por Toketsu » Ter Mar 27, 2012 16:26
- 1 Respostas
- 1168 Exibições
- Última mensagem por fraol

Ter Mar 27, 2012 18:42
Logaritmos
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1856 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
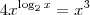

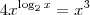

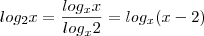 , não se esqueça de cuidar com as condições de existência.
, não se esqueça de cuidar com as condições de existência.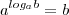

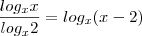
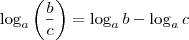






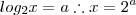
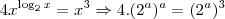
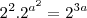
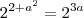
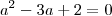
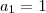
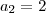
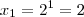
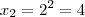



 .
.
 :
: