 por Danilo » Ter Ago 14, 2012 20:19
por Danilo » Ter Ago 14, 2012 20:19
Determine o menor valor da expressão
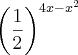
Sei que quanto maior o valor do expoente, menor é o valor da base. E que neste caso o expoente tem de ter um valor positivo (me corrijam se eu estiver errado.). Mas eu não consigo aplicar essas informações no problema.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Ter Ago 14, 2012 21:23
por e8group » Ter Ago 14, 2012 21:23
Minha solução :
Considerem as funções
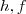
.Donde ,
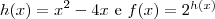
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,
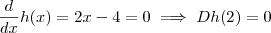
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde
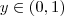
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Danilo » Ter Ago 14, 2012 22:48
por Danilo » Ter Ago 14, 2012 22:48
santhiago escreveu:Minha solução :
Considerem as funções
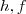
.Donde ,
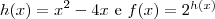
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,
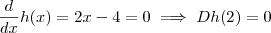
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde
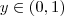
Espero que ajude .
Santhiago, obrigado pela resposta ! Mas vc poderia me ajudar sem utilizar os conceitos vistos no ensino superior?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Ter Ago 14, 2012 23:54
por e8group » Ter Ago 14, 2012 23:54
Sim .
Vamos por etapas.
1)
![\left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x} \left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x}](/latexrender/pictures/af0ff0c3c944a7b1469cfa536769a1a0.png)
2) Sejam
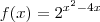
}, onde podemos resscrever que

.
3)Esta parte é analisar o comportamento da função

cujo objetivo é determinar o menor valor de

.
3.1 ) Note que ,
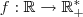
.Assim sabemos que o menor valor da função f estar entre 0 e 1 .
3.2) Seja x_0 o menor valor da função f .onde f(x_0) \in (0,1) .
Para determinarmos
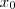
precisamos encontar o menor valor da função h .Para isto veja que h é uma função quadrática ,sendo assim podemos encontar menor "valor" pelo vertice da parábola de onde a teoria diz ,
Vertc.pará. =
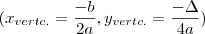
.
Conclusão ,
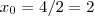
e
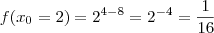
.
OBS.: Para uma leitura sobre funções quadráticas visite(
http://pt.wikipedia.org/wiki/Fun%C3%A7% ... %C3%A1tica).Vale apena .
Obs.: A resposta estar de acordo com o gabarito ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Ter Ago 14, 2012 23:54
por MarceloFantini » Ter Ago 14, 2012 23:54
Você precisa encontrar o mínimo de
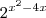
. Note que isto será mínimo quando o expoente for mínimo, pois sabemos que a função exponencial é monotonamente crescente, ou seja, se
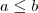
então
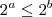
. O mínimo do expoente será o vértice da parábola
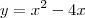
, que acontece em

, portanto o mínimo será
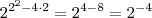
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 3896 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5437 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 2996 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 4982 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
-
- Função Exponencial
por Aline » Seg Jun 29, 2009 18:59
- 3 Respostas
- 5777 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 22:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
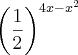

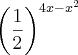

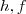 .Donde ,
.Donde , 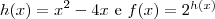 .Assim o menor valor da função f será o minimo absoluto da função h .Então ,
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,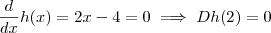 . Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde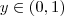

.Donde ,
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde

![\left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x} \left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x}](/latexrender/pictures/af0ff0c3c944a7b1469cfa536769a1a0.png)
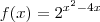 }, onde podemos resscrever que
}, onde podemos resscrever que  .
. cujo objetivo é determinar o menor valor de
cujo objetivo é determinar o menor valor de  .
.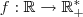 .Assim sabemos que o menor valor da função f estar entre 0 e 1 .
.Assim sabemos que o menor valor da função f estar entre 0 e 1 .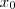 precisamos encontar o menor valor da função h .Para isto veja que h é uma função quadrática ,sendo assim podemos encontar menor "valor" pelo vertice da parábola de onde a teoria diz ,
precisamos encontar o menor valor da função h .Para isto veja que h é uma função quadrática ,sendo assim podemos encontar menor "valor" pelo vertice da parábola de onde a teoria diz ,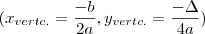 .
.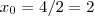 e
e 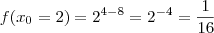 .
.
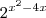 . Note que isto será mínimo quando o expoente for mínimo, pois sabemos que a função exponencial é monotonamente crescente, ou seja, se
. Note que isto será mínimo quando o expoente for mínimo, pois sabemos que a função exponencial é monotonamente crescente, ou seja, se 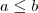 então
então 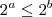 . O mínimo do expoente será o vértice da parábola
. O mínimo do expoente será o vértice da parábola 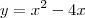 , que acontece em
, que acontece em  , portanto o mínimo será
, portanto o mínimo será 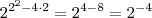 .
.






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.