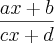 satisfaz f(f(x))=x ,
satisfaz f(f(x))=x , x
xEu tinha feito o seguinte:
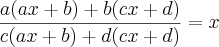
Daí
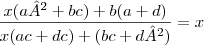
Como no denominador não poderia ter x,fiz que ac+dc = 0 e obtive que a=-d
Enfim,fiquei parada nisso,alguém tem alguma sugestão de como resolver isso?
Obrigada

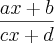 satisfaz f(f(x))=x ,
satisfaz f(f(x))=x , x
x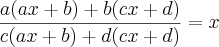
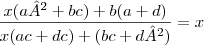

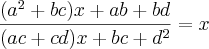
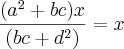



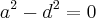
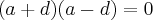
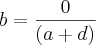 ========>
========> 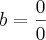 , ou seja, indeterminado!
, ou seja, indeterminado!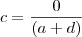 ========>
========> 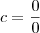 , ou seja, indeterminado!
, ou seja, indeterminado!
danjr5 escreveu:Seguindo de onde parou...
Além do coeficiente de x (denominador) ser zero, o termo independente do numerador também é zero.
Então,
ab + bd = 0
ac + cd = 0
b(a + d) = 0 =========>========>
, ou seja, indeterminado!
c(a + d) = 0 =========>========>
, ou seja, indeterminado!
Podemos concluir que quando (a + d) = 0, b e c pode assumir diversos valores. Quero dizer que:
escolha um valor qualquer para a, o valor de d deverá ser o simétrico de a (lembre-se que a soma deles é zero), escolha um valor qualquer para b, e um valor qualquer para c.
Agora Fraam, termine o exercício quando a = d
Espero ter ajudado, caso contrário, sinta-se à vontade para retornar!


danjr5 escreveu:Fraam,
vc leu a solução??


danjr5 escreveu:Provavelmente sim.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

