Bom dia Bárbara !! Tudo bem ??
Vejamos se posso lhe ajudar.. Esse me parece um típico problema de otimização...
Sejam a e b os lados da sua cerca, como você irá utilizar o muro como um lado também (por economia) então o seu perímetro será
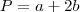
, logo temos:
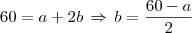
A sua área será:
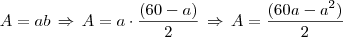
Aqui já temos a área em função de um dos lados (letra a), o gráfico é fácil verificar que será uma parábola com vértice em (30,450), sendo que sua concavidade é para baixo, pois o coeficiente líder da parábola é negativo...
As dimensões para que o terreno tenha área máxima você pode resolver de duas formas, uma é usando o cálculo (faça a derivada da área em função de a e estude seu sinal para achar o ponto de máximo da função) ou, simplesmente, perceba que o vértice já é o ponto de máximo da sua função, sendo a = 30 para uma área máxima, mas essa análise usando o vértice só vale pois o vértice está no primeiro quadrante (isto é, a é positivo), caso contrário teria que derivar a área em função de a para saber o ponto de máximo dentro do primeiro quadrante (isto é, seria um máximo local e não global como no caso do vértice).
Espero ter ajudado...
[ ] 's
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...


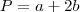 , logo temos:
, logo temos: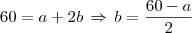
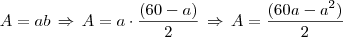

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.