Os biólogos observaram que a taxa de canto dos grilos em uma certa espécie aparentemente
está relacionada com a temperatura. A tabela a seguir mostra as taxas de canto para várias temperaturas.
T(Fº) |50 |55 |60 |65 |70
Taxa |16 |41 |79 |102 |135
a)Faça um gráfico e identifique o modelo que melhor se ajusta aos dados.
b)Encontre uma equação que representa o modelo.
c)IUse o modelo encontrado para estimar a taxa de canto a 100º
O gráfico está no arquivo em JPG anexado ao post.
O modelo, a primeira olhada, é uma função do tipo y = ax + b, até aí, tudo bem. Mas o problema é q não estou conseguindo encontrar uma equação q englobe todos os períodos do gráfico. Já tentei equação da reta e tudo mais, mas não tow conseguindo. Se eu fizer um sistema por período, até consigo, mas apenas para os valores deste período. Como seria essa equação, como é pedido no enunciado na letra "b)"?
Alguém para dar uma dica?


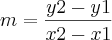



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)