 por joaofonseca » Sáb Abr 30, 2011 13:01
por joaofonseca » Sáb Abr 30, 2011 13:01
Seja a seguinte função polinomial:
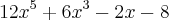
Sabemos que pelo teorema das raizes racionais existe um número racional

irredutivel. Sabemos também que
p pode ser um dos fatores de

e
q pode ser um dos fatores de

.
Assim ficamos com uma lista das possíveis raízes racionais deste polinomio:
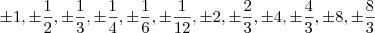
Graficamente a função tem raiz real em 0,866. Ora nenhuma destas frações resulta em 0,866. Posso então concluir que a(s) raizes desta função não são racionais!
Existe alguma técnica algébrica de decompor este polinomio de grau 5?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por FilipeCaceres » Sáb Abr 30, 2011 13:20
por FilipeCaceres » Sáb Abr 30, 2011 13:20
Seja a seguinte função polinomial:
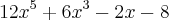
Poste o enunciado completo.
Você deseja apenas fatorar essa função?
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por joaofonseca » Sáb Abr 30, 2011 13:48
por joaofonseca » Sáb Abr 30, 2011 13:48
O enunciado é:
"Encontre os possíveis zeros utilizando o Teorema das Raizes Racionais."
Como eu não encontrei nenhum utilizando este teorema, deduzi que os zeros ou são irracionais ou imaginários. Pensei que decompondo este polinomio em polinomios de 2º grau, seria facíl encontrar os zeros, mesmo que imaginários. A minha dificuldade está mesmo em decompor o polinomio (grau 5).
A ajuda que eu estou pedindo é na decomposição do polinomio, de forma a encontrar as raizes, sejam irracionais ou imaginárias.
Obrigado
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DÚVIDA] Potências de expoentes racionais e raízes.
por invader_zim » Ter Fev 12, 2013 11:31
- 3 Respostas
- 2355 Exibições
- Última mensagem por DanielFerreira

Ter Fev 12, 2013 12:24
Aritmética
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8123 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2583 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- Numeros racionais
por silvia fillet » Qua Out 19, 2011 20:06
- 369 Respostas
- 306691 Exibições
- Última mensagem por Estrela_36

Sáb Dez 03, 2011 17:41
Equações
-
- números: racionais
por Victor Gabriel » Dom Mai 12, 2013 14:35
- 0 Respostas
- 3227 Exibições
- Última mensagem por Victor Gabriel

Dom Mai 12, 2013 14:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
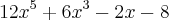
 irredutivel. Sabemos também que p pode ser um dos fatores de
irredutivel. Sabemos também que p pode ser um dos fatores de  e q pode ser um dos fatores de
e q pode ser um dos fatores de  .
.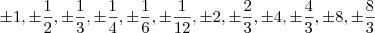




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.