Preciso de ajuda no estudo desta função:
f(x)=
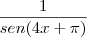
Até agora cheguei a conclusão que:
- Domínio é |R \ {
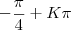}- Contra dominio = ]-?-1] ? [1, +?]
- Não tem zeros. (equaçao deu impossível)
- É ímpar. ( provei que
)- Período é
- Não tem função inversa (pq não é injectiva)
Falta me ver:
Se é ou não continua, se é diferenciavel, ver os intervalos de monotonia, os extremos, o sentido de concavidade, e as assimptotas.
E um exemplo dum problema da 'vida real' para esta função ...
Tenho de provar tudo com cálculos...
Agradeço qualquer correcção/explicação/ajuda em qualquer um destes tópicos, é um bocado urgente ...
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.