 por Helise » Qua Mai 26, 2010 19:21
por Helise » Qua Mai 26, 2010 19:21
Um grupo de alunos da Uniterci programou uma viagem que custaria um total de 900 reais. Algumas semanas antes da partida, duas pessoas se juntaram ao grupo, e cada participante pagou 75 reais a menos. Qual era o número de pessoas que inicialmente fariam a viagem?
-
Helise
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Mai 26, 2010 19:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: agronomia
- Andamento: cursando
 por Molina » Qua Mai 26, 2010 19:39
por Molina » Qua Mai 26, 2010 19:39
Boa tarde, Helise.
Talvez a maior dificuldade deste problema é montar as equações. Chamaremos de
x o número de pessoas que inicialmente fariam a viagem. Pelo enunciado temos que:
x pessoas pagarão r$ 900

1 pessoa pagará
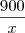 (equação 1)
(equação 1)e
(x+2) pessoas pagarão r$ 900

1 pessoa pagará
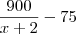 (equação 2)
(equação 2)Este 75 vem da informação do enunciado que diz que eles terão esse desconto com os novos participantes da viagem.
Igualando as equações 1 e 2, temos:
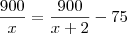
Resolvemos isso multiplicando cruzado e caindo numa equação do 2° grau.
Usando o método de achar raízes que você aprendeu, encontrará um valor negativo e um positivo. Descarte o negativo e fique apenas com

.
Caso não ache esse valor informe e diga até onde chegou.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadrática
por Ananda » Sex Mar 28, 2008 16:00
- 6 Respostas
- 9233 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 21:25
Funções
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2633 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2014 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2094 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8042 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 1 pessoa pagará
1 pessoa pagará 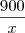 (equação 1)
(equação 1) 1 pessoa pagará
1 pessoa pagará 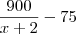 (equação 2)
(equação 2)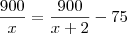
 .
.

