1) Ao analisar a função real definida por
 , podemos afirmar que é injetora? Justifique sua resposta.
, podemos afirmar que é injetora? Justifique sua resposta.
 , podemos afirmar que é injetora? Justifique sua resposta.
, podemos afirmar que é injetora? Justifique sua resposta.

 são injetoras, porque não existem duas imagens iguais para abscissas diferentes.
são injetoras, porque não existem duas imagens iguais para abscissas diferentes. ou
ou 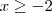 , pois -2 é o vértice da parábola, garantindo que não haja imagens iguais.
, pois -2 é o vértice da parábola, garantindo que não haja imagens iguais.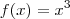 . Domínio da função:
. Domínio da função:  , ou seja, está definida nos reais levando nos reais. Conjunto imagem:
, ou seja, está definida nos reais levando nos reais. Conjunto imagem: 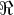 . O conjunto do contra-domínio coincide com o da imagem, e portanto ela é sobrejetora.
. O conjunto do contra-domínio coincide com o da imagem, e portanto ela é sobrejetora. , onde
, onde  é a função identidade. Como ler isso: a composta de g com f é igual à composta de f com g que é igual à função identidade.
é a função identidade. Como ler isso: a composta de g com f é igual à composta de f com g que é igual à função identidade.

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.