Tem razão. A letra (a) é assim mesmo que se raciocina.
Na letra b, temos que analisar a equação
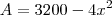
Veja bem, x não poderá assumir valores negativos pois estamos trabalhando com quadrados de dimensões x e portanto x deverá ser maior ou igual à zero.
O maior valor que x poderá assumir ocorre quando
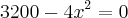
e isto ocorre quando
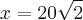
onde já excluí todos os valores negativos.
Assim, os valores para os quais x faz com que a área do retângulo seja maior que 0 até seu máximo, 3200 se encontra no intervalo
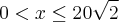
Perceba que x deverá ser um valor maior que zero pois se fosse zero, nao teriamos quadrado algum nos vértices do retângulo. Quanto a ser
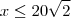
podemos dizer que é válida, pois caso x assuma um valor igual à este valor máximo, teremos utilizado toda a área do retângulo original.
Assim, o intervalo procurado é aberto em zero e fechado a direita, ou seja:
![]0,20\sqrt{2}] ]0,20\sqrt{2}]](/latexrender/pictures/b1098e10fee1a8641072f33af2966836.png)
Perceba que a resposta não é a mesma que seu gabarito. Se no enunciado tivesse sido dito que x assumiria apenas valores inteiros, então a resposta do gabarito estaria correta, porém, como nada foi dito no enunciado, assumi que x seja um número real e portanto, a resposta deveria ser essa, à não ser que eu tenha cometido algum engano, mas creio que não.
Espero ter ajudado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali


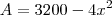
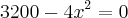
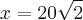
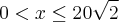
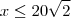
![]0,20\sqrt{2}] ]0,20\sqrt{2}]](/latexrender/pictures/b1098e10fee1a8641072f33af2966836.png)


 .
.
 :
: