Ajuda questão de matemática da fuvest

por **gabriela o marengao** » Qui Fev 13, 2014 21:22

60 - O número de pontos comuns aos gráficos das funções f(x)= x^4 + 3 e g(x) = -x^2 + 2x é
a) 4
b) 3
c) 2
d) 1
e) 0

Agradeço desde já.

por **e8group** » Qui Fev 13, 2014 21:57

Dica :

Se l > 0

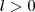é o valor mínimo que f(x)

assume ,então o gráfico da função estar sempre acima da reta y= l

.

Se

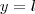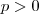é o valor máximo que g(x)

assume , então o gráfico da função estar sempre abaixo da reta y = p

.

Faça o esboços das curvas que notará isto .

Uma condição para que exista pelo menos um ponto comum entre os gráficos é que $l \leq p$ .

E quem são p, l

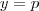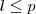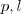? Para determinar

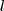é fácil , ora estamos sempre add um número positivo a 3 , supondo x differente de zero .Logo , o menor valor que f(x)

assume é 3 e isto ocorre quando x = 0

.
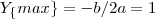E para encontra p , podemos aplicar a fórmula $Y_\{max\} = -b/2a = 1$ (quando a < 0) em que a = -1 [/tex ]e [tex] b = 2

. Alternativamente , completando quadrados

g(x) = -x^2 + 2x = -(x^2 - 2x) = -([x^2 -2x +1] -1) = -([x-1]^2 - 1) = -[x-1]^2 +1

.

Agora observe que estamos sempre add um número negativo a 1 ,supondo x differente de zero . Logo , o valor máximo que g(x)

assume é

.

Agora tente concluir .

Ajuda questão de matemática da fuvest

Ajuda questão de matemática da fuvest

Ajuda questão de matemática da fuvest

Re: Ajuda questão de matemática da fuvest

Quem está online