 por SILMARAKNETSCH » Qua Nov 14, 2012 18:08
por SILMARAKNETSCH » Qua Nov 14, 2012 18:08
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por SILMARAKNETSCH » Qua Nov 14, 2012 22:05
por SILMARAKNETSCH » Qua Nov 14, 2012 22:05
SILMARAKNETSCH escreveu:![f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5 f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5](/latexrender/pictures/a41ba6241bced61ca103a3b14e63d623.png)
raiz os amigos ja me ensinaram mas a parte de frações junto complicou.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
 por MarceloFantini » Qua Nov 14, 2012 22:29
por MarceloFantini » Qua Nov 14, 2012 22:29
Acredito que a função seja
![f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5 f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5](/latexrender/pictures/d44e64bddeb47b3fa7c99a3aca911adf.png)
.
Vamos reescrevê-la da seguinte forma:
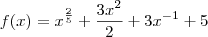
.
Derivando, vamos usar alguns fatos:
Primeiro, a derivada de
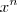
, para qualquer

real, é
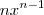
.
Segundo, a derivada de uma constante é zero.
Aplicando isto, segue que
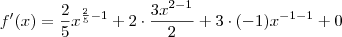
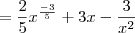
.
Se encontrar alguma dificuldade, refaça as contas no papel, ajuda bastante.
Editado pela última vez por
MarceloFantini em Qui Nov 15, 2012 08:25, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SILMARAKNETSCH » Qui Nov 15, 2012 08:07
por SILMARAKNETSCH » Qui Nov 15, 2012 08:07
sIM É O QUE TENHO FEITO REFAÇO NO PAPEL ESTOU COM MIL FOLHAS AQUI ESTOU A UM MÊS JA RABISCANDO EXERCÍCIOS AGORA SEMANA QUE VEM É A PROVA CONSEGUI NA FACULDADE UMA AULA PRESENCIAL ANTES DA PROVA TB PARA TODA NOSSA TURMA AQUI FINDA MINHA MATÉRIA DESSE BIMESTRE MAS COMO QUERO PASSAR NO CONCURSO DO TRE ESTAREI AQUI CONTINUAMENTE AGRADEÇO A AJUDA SEM ELA NÃO CHEGARIA A LUGAR ALGUM ENSINO A DISTÂNCIA TEM QUE TER MUITA GARRA E CORRER ATRÁS SENÃO É IMPOSSÍVEL APRENDER MATEMÁTICA SÓ O PROFESSOR É INDISPENSÁVEL OBRIGADO PROFESSOR.
-
SILMARAKNETSCH
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Seg Out 29, 2012 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: administração EAD prouni deficiente físi
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Logaritmo com raiz e frações
por _Liilo » Ter Nov 02, 2010 16:11
- 5 Respostas
- 27036 Exibições
- Última mensagem por _Liilo

Ter Nov 02, 2010 19:39
Logaritmos
-
- [Frações Algébricas] Como simplifico essa fração?
 por Kah » Qua Mar 18, 2015 17:44
por Kah » Qua Mar 18, 2015 17:44
- 1 Respostas
- 2166 Exibições
- Última mensagem por Russman

Qua Mar 18, 2015 22:38
Álgebra Elementar
-
- proporção mistura de substância
por hevhoram » Qui Jun 23, 2011 14:15
- 1 Respostas
- 4460 Exibições
- Última mensagem por FilipeCaceres

Qui Jun 23, 2011 15:30
Álgebra Elementar
-
- Ajuda com essa função
por andreagenor » Qui Nov 11, 2010 03:11
- 6 Respostas
- 4315 Exibições
- Última mensagem por rogeriomoreira

Sáb Nov 20, 2010 17:56
Funções
-
- Ajuda com essa função
por andre2908 » Ter Jul 15, 2014 02:15
- 2 Respostas
- 1860 Exibições
- Última mensagem por andre2908

Ter Jul 22, 2014 13:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5 f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5](/latexrender/pictures/a41ba6241bced61ca103a3b14e63d623.png)




![f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5 f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5](/latexrender/pictures/d44e64bddeb47b3fa7c99a3aca911adf.png) .
.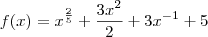 .
.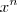 , para qualquer
, para qualquer  real, é
real, é 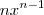 .
.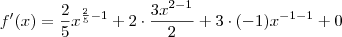
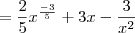 .
.




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.