Acredito que a função seja
![f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5 f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5](/latexrender/pictures/d44e64bddeb47b3fa7c99a3aca911adf.png)
.
Vamos reescrevê-la da seguinte forma:
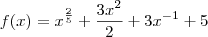
.
Derivando, vamos usar alguns fatos:
Primeiro, a derivada de
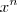
, para qualquer

real, é
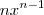
.
Segundo, a derivada de uma constante é zero.
Aplicando isto, segue que
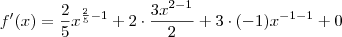
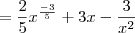
.
Se encontrar alguma dificuldade, refaça as contas no papel, ajuda bastante.
![f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5 f(x) = \sqrt[5]{x²} + \frac{3}{2}x² + \frac{3}{x} + 5](/latexrender/pictures/a41ba6241bced61ca103a3b14e63d623.png)




![f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5 f(x) = \sqrt[5]{x^2} + \frac{3x^2}{2} + \frac{3}{x} +5](/latexrender/pictures/d44e64bddeb47b3fa7c99a3aca911adf.png) .
.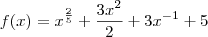 .
.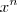 , para qualquer
, para qualquer  real, é
real, é 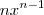 .
.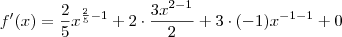
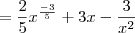 .
.

