na função f(x)=3x-2,sabemos que f(a)=b-2 e f(b)=2b+a. o valor de f[f(a)] é:
a-)a
b-)1
c-)0
d-)-1
e)-2
eu fiz o resultado tinha dado 2b-8,tentei dinovo e deu 3b-2
acho que eu to fazendo tudo errado,me ajuda aew
valeu!



natanskt escreveu:na função f(x)=3x-2,sabemos que f(a)=b-2 e f(b)=2b+a. o valor de f[f(a)] é:
a-)a
b-)1
c-)0
d-)-1
e)-2
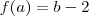 --------------->
--------------->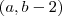
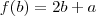 ------------->
------------->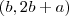
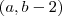
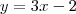
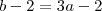
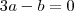
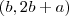
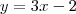

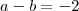
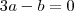

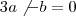
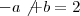
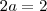

![f[f(a)]=f[1]=1 f[f(a)]=f[1]=1](/latexrender/pictures/144449d02c052bf03ce56e3d17be52cc.png)

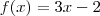
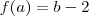
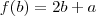
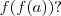
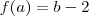 vou colocar o o f(b) no lugar do b
vou colocar o o f(b) no lugar do b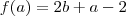 agora vou decobrir f(f(a))
agora vou decobrir f(f(a))
natanskt escreveu:nossa mano,
não intendi é dificil essa questão
olha como eu fiz isso ta certo?vou colocar o o f(b) no lugar do b
agora vou decobrir f(f(a))
2b+a-2=2b+a-2 corta o a com a,-2 com -2
2b=2b
=1
kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
não intendi,vou tentar aprender essa questão


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante