![f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}}](/latexrender/pictures/d2a94274c8ad5615ce947edfd0dbd721.png "f(x)= \sqrt[2]{\frac{(1-x)({x}^{2}-4)}{2x-1}}")
Estou sem o gabarito. Gostaria de conferir se resolvi corretamente.
O meu conjunto domínio, após ter estudado o sinal da função, através do Teorema de Bolzano, foi o seguinte:
D[f(x)] = {
|
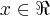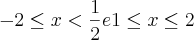}Confere?
por Jonatan » Qua Jul 28, 2010 13:24
|}
por MarceloFantini » Qua Jul 28, 2010 14:51
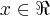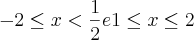Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)