 por Quatroemes » Dom Mar 21, 2010 20:53
por Quatroemes » Dom Mar 21, 2010 20:53
Boa Noite

Não consigo resolver esta equação de forma a obter o resultado apresentado.
Será que alguém me pode dizer onde estou a fazer asneira??
Eu resolvi da seguinte forma:
(X
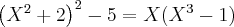
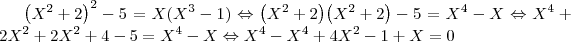
Utilizei a fórmula resolvente sendo a=4 b= 1 c=-1
e o resultado a que chego está longe de ser o conjunto de solução apresentado.
Chego ao seguinte resultado: [/tex]
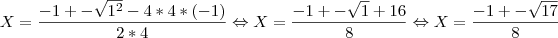
Obrigada!!
-
Quatroemes
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 21, 2010 20:01
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: 9º ano
- Andamento: cursando
 por vyhonda » Seg Mar 22, 2010 08:34
por vyhonda » Seg Mar 22, 2010 08:34
Vendo sua resolução, está OK!! Mas pode ser que o enunciado foi escrito errado, confira. Mas se for isso o enunciado sua resposta esta correta.
-
vyhonda
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jan 17, 2010 20:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Materiais - Unesp
- Andamento: cursando
 por Quatroemes » Seg Mar 22, 2010 11:34
por Quatroemes » Seg Mar 22, 2010 11:34
Muito Obrigada!!
De facto por mais que tente não consigo obter outro resultado, o conjunto de solução apresentado nas soluções é 1/2 e 1/4, valores aos quais eu não consigo chegar!!
Já verifiquei o enunciado e de facto está correcto

Ainda bem que devem ser as soluções erradas pois já estava a ficar assustada de tentar tantas vezes e não conseguir acertar.
Mais uma vez muito obrigada pela ajuda!!
Abraço
MMMM
-
Quatroemes
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 21, 2010 20:01
- Formação Escolar: ENSINO FUNDAMENTAL I
- Área/Curso: 9º ano
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equações de 2º grau
por Lismara » Seg Ago 31, 2009 23:25
- 4 Respostas
- 2854 Exibições
- Última mensagem por Lismara

Ter Set 01, 2009 21:42
Sistemas de Equações
-
- equacoes do 2 Grau
por guillcn » Qui Jun 30, 2011 12:30
- 1 Respostas
- 1603 Exibições
- Última mensagem por joaofonseca

Qui Jun 30, 2011 15:25
Equações
-
- equaçoes do 1 grau
por thalia alexandrina » Seg Out 10, 2011 14:29
- 3 Respostas
- 3027 Exibições
- Última mensagem por MarceloFantini

Ter Out 11, 2011 23:06
Sistemas de Equações
-
- Equações do 3º grau
por baianinha » Qua Mar 14, 2012 16:09
- 3 Respostas
- 2271 Exibições
- Última mensagem por nicolegcg

Ter Jun 12, 2012 14:47
Sistemas de Equações
-
- Equações de 3º grau
por nicolegcg » Seg Jun 11, 2012 17:50
- 4 Respostas
- 2893 Exibições
- Última mensagem por nicolegcg

Ter Jun 12, 2012 14:45
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
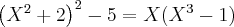
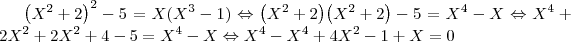
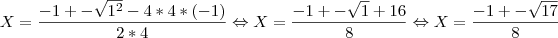




 .
.
 :
: