Tenho uma dúvida quanto à idéia final duma questão.
Seu enunciado apenas diz: "Se a e b são números reais tais que
![\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13} \sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}}=\sqrt[2]{13}](/latexrender/pictures/231a482ada01239aeb61a385c37cc927.png) , quanto vale
, quanto vale ![\left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right| \left|\sqrt[2]{\frac{a}{b}}-\sqrt[2]{\frac{b}{a}} \right|](/latexrender/pictures/f620f4a8e0030886907861db4ec387cd.png) ?"
?"Então, eu comecei pela primeira expressão jogando a raiz quadrada do valor "13" para o outro lado:
![\left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13 \left(\sqrt[2]{\frac{a}{b}}+\sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/b53e050df01a58dad78f344a69249aae.png)
Em seguida fui fazendo a resolução comum:
![\left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13 \left( \sqrt[2]{\frac{a}{b}} \right)^2+2*\sqrt[2]{\frac{a}{b}}*\sqrt[2]{\frac{b}{a}}+\left( \sqrt[2]{\frac{b}{a}} \right)^2=13](/latexrender/pictures/387f64fa1bfb8eea1300c4068230ac3b.png)




Logo...

Daí então não consegui complementar a idéia.
Caro professor:
Será que o Senhor pode me ajudar a terminá-la? Ou ainda me dizer se esta idéia não tem fundamento pra achar a resposta em questão?
Agradeço sua atenção e espero resposta.




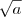 em cima e embaixo, e fazendo o mesmo processo na segunda só que multiplicando por
em cima e embaixo, e fazendo o mesmo processo na segunda só que multiplicando por  , temos:
, temos:

 dos dois lados:
dos dois lados:


 dos dois lados:
dos dois lados:



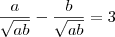








 :
:




 .
.



