 por osmarioe » Sex Mai 01, 2015 19:20
por osmarioe » Sex Mai 01, 2015 19:20
Desenhar os gráficos cartesianos de y= -2x-7 e de y= 4x+5 e determinar o ponto comum a eles.
resolução:
y= -2x-7 tem coeficiente linear -7 e raiz - 7/2
y= 4x+5 tem coeficiente linear 5 e raiz -5/4
resolvendo o sistema:
y= -2x-7
y= 4x+5
obtendo x = -2 e y= -3
portanto, o ponto comum as duas retas é A( -2; -3)
Não entendi como ele chegou a esse valor da resolução do sistema de x= -2 e y= -3?
-
osmarioe
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 26, 2015 22:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Sáb Mai 02, 2015 00:19
por Cleyson007 » Sáb Mai 02, 2015 00:19
Olá, boa noite!
Concorda comigo que o ponto em comum tem coordenadas x e y e pode ser escrito como P = (x,y)?
Esses valores de x e y (coordenadas do ponto P) são obtidos resolvendo o sistema de equações do primeiro grau:
y= -2x - 7
y = 4x + 5
Como y = y, vou igualar a primeira equação com a segunda, obtendo:
-2x - 7 = 4x + 5
-2x - 4x = 5 + 7
-6x = 12
x = -12/6
x = -2Para encontrar o valor de y basta aplicá-lo em qualquer uma das equações. Vamos na primeira:
y= -2x - 7 -----> y = -2(-2) - 7 = 4 - 7 ----->
y = -3Se caso desejar conhecer o meu trabalho melhor por favor entre em contato: (38) 9889-5755 (WhatsApp)
email:
descomplicamat@hotmail.comQualquer dúvida estou a disposição.
Bons estudos

- Anexos
-
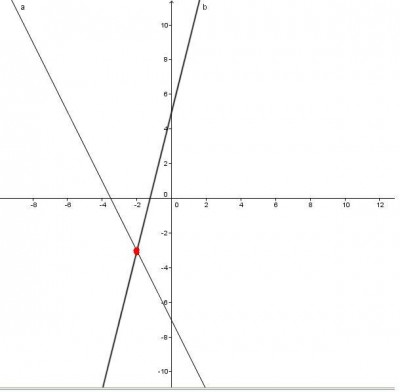
- Ponto em Comum
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por osmarioe » Sáb Mai 02, 2015 14:21
por osmarioe » Sáb Mai 02, 2015 14:21
Cleyson007 escreveu:Olá, boa noite!
Concorda comigo que o ponto em comum tem coordenadas x e y e pode ser escrito como P = (x,y)?
Esses valores de x e y (coordenadas do ponto P) são obtidos resolvendo o sistema de equações do primeiro grau:
y= -2x - 7
y = 4x + 5
Como y = y, vou igualar a primeira equação com a segunda, obtendo:
-2x - 7 = 4x + 5
-2x - 4x = 5 + 7
-6x = 12
x = -12/6
x = -2Para encontrar o valor de y basta aplicá-lo em qualquer uma das equações. Vamos na primeira:
y= -2x - 7 -----> y = -2(-2) - 7 = 4 - 7 ----->
y = -3Se caso desejar conhecer o meu trabalho melhor por favor entre em contato: (38) 9889-5755 (WhatsApp)
email:
descomplicamat@hotmail.comQualquer dúvida estou a disposição.
Bons estudos

Entendi, muito obrigado pela explicação Cleyson007

-
osmarioe
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Abr 26, 2015 22:05
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3093 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- Como resolvo esse sistema
por leoparo » Ter Fev 15, 2011 20:52
- 1 Respostas
- 1863 Exibições
- Última mensagem por Molina

Qua Fev 16, 2011 10:33
Sistemas de Equações
-
- Como resolver esse sistema linear
por Silva339 » Qua Mar 20, 2013 18:14
- 1 Respostas
- 1870 Exibições
- Última mensagem por Russman

Qua Mar 20, 2013 18:46
Sistemas de Equações
-
- Como achar esse valor seno?
por angsrom » Qua Ago 03, 2011 09:21
- 2 Respostas
- 1993 Exibições
- Última mensagem por supertag

Qui Ago 04, 2011 01:18
Geometria Plana
-
- como resolvo esse problema de sistema de equação?
por kellen e winicius » Ter Ago 30, 2011 00:13
- 3 Respostas
- 5089 Exibições
- Última mensagem por Caradoc

Ter Ago 30, 2011 20:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




