 por Andressa Colare » Sex Abr 17, 2015 17:28
por Andressa Colare » Sex Abr 17, 2015 17:28
Me ajudem galera, é uma questão de trabalho, e é PRA SEGUNDA é questão de vida ou morte "a função f: R-R definida por f(x): -(3p-1)x² +7x, tem a concavidade voltada para baixo. Quais valores reais podem substituir p?"
-
Andressa Colare
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 17, 2015 13:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sex Abr 17, 2015 20:36
por DanielFerreira » Sex Abr 17, 2015 20:36
Olá
Andressa, seja bem-vinda!
Seja
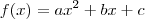
uma função de grau dois, onde

; temos que:
- a concavidade da parábola será voltada para baixo se

; e,
- a concavidade será voltada para cima se

.
Tente concluir a partir do que fora exposto!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3429 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4199 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [Funções] questões de funções
por Zandrojr » Qua Ago 31, 2011 11:39
- 0 Respostas
- 3141 Exibições
- Última mensagem por Zandrojr

Qua Ago 31, 2011 11:39
Funções
-
- Funções
por Revelants » Dom Out 05, 2008 15:07
- 1 Respostas
- 3393 Exibições
- Última mensagem por Molina

Dom Out 05, 2008 15:53
Cálculo: Limites, Derivadas e Integrais
-
- Funçoes
por Luna » Seg Set 28, 2009 20:02
- 1 Respostas
- 2998 Exibições
- Última mensagem por Marcampucio

Seg Set 28, 2009 21:35
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



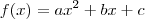 uma função de grau dois, onde
uma função de grau dois, onde  ; temos que:
; temos que: ; e,
; e, .
.