




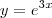 é um conjunto munido de elementos
é um conjunto munido de elementos 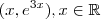 e da função constante ,
e da função constante , 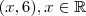 . Estes gráficos se intersectam quando existe x real tal que ocorra a igualdade
. Estes gráficos se intersectam quando existe x real tal que ocorra a igualdade 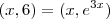 .Devemos encontrar x que cumpre com
.Devemos encontrar x que cumpre com 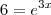 . Aplicando o logaritmo natural em ambos lados da igualdade, obterá um único x que satisfaça a igualdade , consequentemente terá apenas um par ordenado .
. Aplicando o logaritmo natural em ambos lados da igualdade, obterá um único x que satisfaça a igualdade , consequentemente terá apenas um par ordenado . 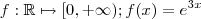 é fácil verificar que a função
é fácil verificar que a função  é bijetora ( injetora e sobrejetora e portanto inversível ) , isso significa que para cada número
é bijetora ( injetora e sobrejetora e portanto inversível ) , isso significa que para cada número  em
em 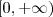 existe um único
existe um único 
 em
em  tal que
tal que  .
.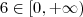 , portanto existe um único
, portanto existe um único  real para o qual
real para o qual 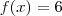 , logo a interseção entre os gráficos das funções possuem apenas 1 elemento .
, logo a interseção entre os gráficos das funções possuem apenas 1 elemento .
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

