 por kellykcl » Qui Abr 10, 2014 20:18
por kellykcl » Qui Abr 10, 2014 20:18
Boa noite galera do fórum!
Mais uma vez precisando da ajuda de vocês!
Determine o domínio das seguintes funções:
1)
![f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}} f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}}](/latexrender/pictures/2ca0cc4c086c319df690d96cabd60891.png)


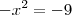
![x=\sqrt[]{9} x=\sqrt[]{9}](/latexrender/pictures/e3bba98047539d564c787e8b39fbef97.png)
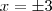


2)
![f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x} f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x}](/latexrender/pictures/57d12ed478b1ca4cff834f7d003fce23.png)
Gabarito:

Obs.:Não sei como resolver esta última questão, como o denominador tem que ser

0, não estou sabendo esboçar o gráfico!

Gostaria de saber se a primeira está correta (não tenho gabarito) e também como fazer a segunda incluindo o gráfico!
Desde já agradeço a colaboração!
"Quem ensina aprende ao ensinar e quem aprende ensina ao aprender."
(Paulo Freire)
-
kellykcl
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Fev 15, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
 por kellykcl » Sex Abr 11, 2014 14:15
por kellykcl » Sex Abr 11, 2014 14:15
Lucio Carvalho escreveu:Ola kellykcl,
Segue, em anexo, uma possível ajuda.
Lúcio
Obrigada pela tentativa, mas minha dificuldade é que por serem duas inequações do 2º grau, encontramos 4 raízes ( 2 raízes de uma e duas da outra, embora com o mesmo resultado: 0 e -1) , difícil explicar onde estou errando pois estou completamente perdida neste exercício!
Você respondeu que no numerador, por ser uma raiz , a condição seria

, porém eu fiz
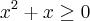
!
Se alguém pudesse me explicar passo a passo ajudaria muito!
Gostaria de saber tb se a primeira está correta!


"Quem ensina aprende ao ensinar e quem aprende ensina ao aprender."
(Paulo Freire)
-
kellykcl
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Fev 15, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4195 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
-
- [domínio] Funcões
por Cleyson007 » Qua Out 29, 2008 00:28
- 2 Respostas
- 2372 Exibições
- Última mensagem por Cleyson007

Seg Jun 01, 2009 12:38
Funções
-
- Funções - Intervalo, Domínio
por jorgeltpereira » Seg Dez 08, 2008 10:33
- 1 Respostas
- 1772 Exibições
- Última mensagem por Neperiano

Qua Ago 24, 2011 15:07
Funções
-
- Funções:Domínio e Imagem
por +Julia » Sáb Abr 12, 2014 09:54
- 0 Respostas
- 1148 Exibições
- Última mensagem por +Julia

Sáb Abr 12, 2014 09:54
Funções
-
- Dominio de funções, ajuda por favor ?
por fabio155nike » Qui Jul 17, 2014 15:58
- 0 Respostas
- 1382 Exibições
- Última mensagem por fabio155nike

Qui Jul 17, 2014 15:58
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}} f(x)=\frac{1}{\sqrt[]{9-{x}^{2}}}](/latexrender/pictures/2ca0cc4c086c319df690d96cabd60891.png)


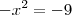
![x=\sqrt[]{9} x=\sqrt[]{9}](/latexrender/pictures/e3bba98047539d564c787e8b39fbef97.png)
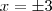


![f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x} f(x)= \frac{\sqrt[]{{x}^{2}+x}}{{x}^{2}+x}](/latexrender/pictures/57d12ed478b1ca4cff834f7d003fce23.png)

 0, não estou sabendo esboçar o gráfico!
0, não estou sabendo esboçar o gráfico! 



 , porém eu fiz
, porém eu fiz 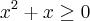 !
!
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.