 por Tixa11 » Dom Nov 11, 2012 13:24
por Tixa11 » Dom Nov 11, 2012 13:24
Como derivo a função
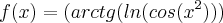
?
Não estou a conseguir...
-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
 por e8group » Dom Nov 11, 2012 14:44
por e8group » Dom Nov 11, 2012 14:44
Nestes casos eu gosto de decompor a função por composição .considerando ,
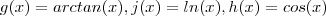
e
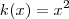
podemos rescrever

como ,
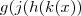
.
Daí ,
![f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x) f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x)](/latexrender/pictures/63bd9456be81f44fc49fc87a6f2306d2.png)
Derivando cada uma em relação a x ,
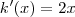
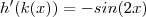
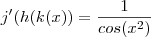
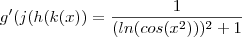
conclusão ,
![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)
Por favor , comente qualquer dúvida .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Tixa11 » Dom Nov 11, 2012 20:05
por Tixa11 » Dom Nov 11, 2012 20:05
santhiago escreveu:Nestes casos eu gosto de decompor a função por composição .considerando ,
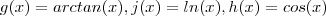
e
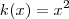
podemos rescrever

como ,
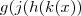
.
Daí ,
![f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x) f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x)](/latexrender/pictures/63bd9456be81f44fc49fc87a6f2306d2.png)
Derivando cada uma em relação a x ,
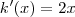
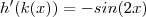
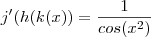
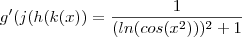
conclusão ,
![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)
Por favor , comente qualquer dúvida .
Muito obrigado pela ajuda. Realmente é muito mais simples assim

-
Tixa11
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Sáb Nov 10, 2012 12:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bioquimica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14798 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3844 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8556 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- derivada de uma função
por jmario » Sex Mai 07, 2010 13:51
- 4 Respostas
- 3797 Exibições
- Última mensagem por Elcioschin

Sex Mai 07, 2010 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
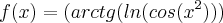 ?
?
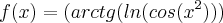 ?
?
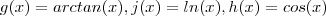 e
e 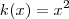 podemos rescrever
podemos rescrever  como ,
como , 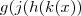 .
. ![f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x) f'(x) = [ g(j(h(k(x) )] ' = g' (j(h(k(x) ) \cdot j'(h(k(x)) \cdot h'( k(x) ) \cdot k'(x)](/latexrender/pictures/63bd9456be81f44fc49fc87a6f2306d2.png)
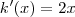
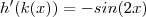
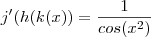
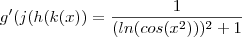
![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)

e
podemos rescrever
como ,
.
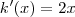
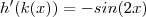
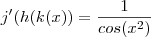
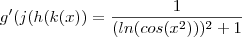
![f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x f'(x) = \frac{1}{[ (ln(cos(x^2) ) )^2 +1 ] } \cdot \frac{1}{cos(x^2) } \cdot (-sin( 2x) ) 2x](/latexrender/pictures/aea40ffb897a36b26b98e11c3db3783f.png)

